Philosophiæ

Naturalis

Principia

Mathematica

(Matematické základy přírodní filosofie)

Isaac Newton

Liber Primus

De Motu Corporum

(O pohybu těles)

Sekce 1.

O metodě prvotních a mezních hodnot, k použití v následujících důkazech .

Lemma 1.

Proměnné veličiny, a též poměry veličin, které se v každém mezním okamžiku trvale blíží k rovnosti, a které se před koncem tohoto okamžiku blíží k sobě tak, že jejich rozdíl je menší než libovolná daná hodnota, se nakonec stávají stejnými .

Pokud by to neplatilo, potom by byly nakonec různé, jejich rozdíl označme D. Potom se nemohou přiblížit k rovnosti tak, aby jejich rozdíl byl menší než D, což je v rozporu s předpokladem.

Lemma 2.

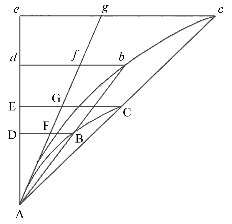
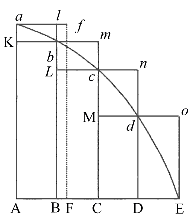Pokud v libovolném diagramu AacE zahrnujícím úsečky Aa a AE a křivku acE, libovolný počet rovnoběžníků Ab, Bc, Cd, … sestrojených nad základnami AB, BC, CD, … a mající strany Bb, Cc, Dd, … rovnoběžné se stranou Aa diagramu, a když jsou doplněny rovnoběžníky aKbl, bLcm, cMdn, … a když šířka těchto těchto rovnoběžníků se zmenšuje a jejich počet nekonečně roste, tvrdím, že mezní plochy jak vepsaného diagramu AKbLcMdD, tak opsaného diagramu AalbmcndoE a křivky AabcdE mají rovné mezní hodnoty.

Jelikož rozdíl mezi vepsaným a opsaným diagramem je součtem rovnoběžníků Kl, Lm, Mn a Do, který má (protože mají stejné základny) stejnou [plochu] jako obdélník se základnou Kb (základna některého z nich) a výškou Aa (součet všech výšek), tj. obdélník ABla. Ale tento obdélník, protože jeho šířka AB nekonečně klesá, se stává menší než libovolný daný obdélník. Proto jsou [plochy] vepsaného diagramu, opsaného diagramu, a navíc i prostředního křivočarého diagramu nakonec stejné. Což se mělo dokázat.

Lemma 3.

Mezní hodnoty odpovídají těmto rovným hodnotám i tehdy, když šířky AB, BC, CD, … rovnoběžníků nejsou stejné a nekonečně se zmenšují .

Nechť je sestrojen rovnoběžník FAaf  tak, že AF je rovno největší šířce. Jeho plocha bude větší než rozdíl vepsaného a opsaného diagramu: pokud ovšem jeho šířka AF  bude nekonečně klesat, bude menší než libovolně zvolený rovnoběžník. Což se mělo dokázat.

Důsledek 1. Proto konečné sloučení mizejících rovnoběžníků splývá s křivočarým diagramem v každém bodě.

Důsledek 2. Kromě toho přímkový diagram vytvořený tětivami mizejících oblouků ab, bc, cd, … splývá nakonec s křivočarým diagramem.

Důsledek 3. Totéž platí o ohraničené přímkový diagram sestavený z tečen těch samých oblouků.

Důsledek 4. A proto konečný diagram (s ohledem na jeho obvod acE) není přímková, ale křivočará hranice přímkových diagramů.

Lemma 4.

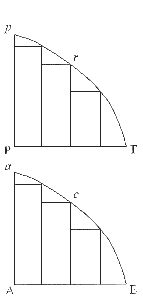Jestliže ve dvou diagramech AacE a PprT jsou vepsány (jako nahoře)  dvě řady rovnoběžníků a počet rovnoběžníků je v obou řadách stejný, a pokud, když jejich šířky nekonečně klesají a mezní poměry [ploch] rovnoběžníků v jednom diagramu a odpovídajících rovnoběžníků v druhém diagramu jsou stejné, potom tvrdím, že [plochy] obou diagramů AacE a PprT jsou navzájem ve stejném vzájemném poměru .

Jelikož jsou si jednotlivé rovnoběžníku na obou diagramech podobné, potom (po sestavení) si odpovídají i jejich součty na jednotlivých diagramech, stejně jako [plochy] jednotlivých diagramů, protože (podle lemy 3) [plocha] prvého diagramu a prvý součet je k [ploše] druhého diagramu a druhému součtu ve stejném poměru. Což se mělo dokázat.

Důsledek. Proto, když jsou dvě veličiny libovolného druhu rozděleny libovolně na stejný počet částí, a tyto části, když jejich počet roste a jejich velikost nekonečně klesá, zachovávají stejný vzájemný poměr, prvá k prvé, druhá k druhé, a tak postupně dále, potom celky budou jeden k druhému ve stejném poměru. Proto když rovnoběžníky v diagramech tohoto lemmatu jsou sestrojeny ve stejném poměru jako tyto části, jejich součet bude stejný jako součet rovnoběžníků, a proto když počet rovnoběžníků roste a jejich velikost se nekonečně zmenšuje, součet částí bude v konečném poměru [ploch] rovnoběžníků v jednom diagramu a odpovídajících rovnoběžníků v druhém, a tedy (podle hypotézy) v konečném poměru jednotlivých částí.

Lemma 5.

Všechny vzájemně si odpovídající strany podobných diagramů, jak přímkových tak křivočarých, jsou si úměrné, a plochy jsou v poměru druhých mocnin jejich stran.

Lemma 6.

Jestliže libovolný oblouk ACB daný svou polohou je protnut tětivou AB v některém bodě A uvnitř spojitého zakřivení a dotýká se ho přímka AD protažená na obě strany, a jestliže se body A a  B přiblíží a dojdou k sobě, tvrdím, že úhel  BAD sevřený tečnou a sečnou se nekonečně zmenší a nakonec vymizí.

Neboť pokud úhel nevymizí, potom úhel sevřený obloukem ACB a tečnou AD bude rovný úhlu obou přímek, a proto zakřivení v bodě A nebude spojité, což je v rozporu s hypotézou.

Lemma 7.

Za stejných předpokladů, tvrdím, že mezní vzájemné poměry oblouku, sečny a tečny jsou si rovny. [x ≈ d  ≈ a]

Nechť se bod B přibližuje k bodu A. Označme body na prodloužení přímek AB a AD jako b a d a přímka bd  nechť je rovnoběžná se sečnou BD  a oblouk Acb je stále podobný ACB. Potom když se bod B přibližuje k bodu A, úhel dAb vymizí (lemma 6), a tak přímky Ab, Ad (které jsou stále konečné) a prostřední oblouk Acb splynou a budou tedy stejné. A tedy přímky AB a AD a prostřední oblouk ACB (které jsou neustále podobné přímkám Ab, Ad a oblouku Acb) též vymizí a budou si navzájem rovnými mezními hodnotami. Což se mělo dokázat.

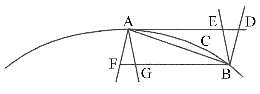Důsledek 1. Tedy, pokud sestrojíme přímku BF  bodem B rovnoběžně s tečnou, která protne libovolnou přímku AF  procházející bodem A, potom BF  bude mít mezní hodnotu rovnou mizejícímu oblouku ACB, protože když doplníme rovnoběžník AFBD, potom BF má mezní hodnotu stejnou mezní hodnotu s AD.

Důsledek 2. A jestliže body B a A  vedeme další přímky BE, BD, AF a AG, které protínají tečnu AD a její rovnoběžku BF, potom mezní hodnoty AD, AE, BF a BG tětivy a oblouk AB jsou si rovny.

Důsledek 3. A tedy všechny tyto přímky je možno navzájem zaměňovat při jakékoliv argumentaci týkající se mezních hodnot.

Lemma 8.

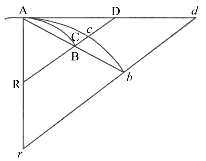
Jestliže dané přímky AR a  BR, oblouk ACB, jeho sečna AB vytvářejí tři trojúhelníky RAB, RACB a  RAD a jestliže se body A a  B navzájem přibližují, tvrdím, že tyto trojúhelníky, když se ztrácejí, jsou ve své mezní formě podobné a jejich mezní hodnoty jsou stejné.

Nechť se B přibližuje k A. Označme body na prodloužení přímek AB, AD a AR jako b, d a r  tak, že rbd je rovnoběžná s RD, nechť oblouk Acb je stále shodný s ACB. Když se body A a B přibližují,potom úhel bAd vymizí a proto trojúhelníky rAb, rAcb a rAd, které zůstávají konečné, splynou a proto jsou podobné a rovné. Proto i RAB, RACB a RAD, které jsou také podobné a úměrné těm předchozím, budou v mezní hodnotě  podobné a stejné. Což se mělo dokázat.

Důsledek. Proto mohou být tyto trojúhelníky navzájem zaměnitelné, pokud jde o mezní hodnoty.

Lemma 9.

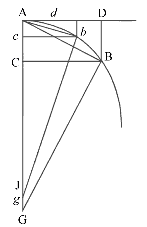
Pokud se přímka AE a křivka ABC, obě v pevné poloze, protínají pod úhlem A, a pokud jsou sestrojeny přímky  BD a CE v pevném úhlu k přímce AE a protínají křivku v bodech  B a C. Potom když se body  B a  C současně blíží bodu A, tvrdím, že plochy trojúhelníků ABD a ACE budou mezně k sobě navzájem jako čtverce jejich stran.

Nechť se body B a C  přibližují k bodu A. Nechť v prodloužení přímky AD leží body d  a e  tak, že Ad  a Ae jsou úměrné  AD a AE, a sestrojme kolmice db a ec  rovnoběžné s DB a EC a protínající prodloužené AB a AC v bodech b a c. Nechť křivka Abc je sestrojena jako podobná křivce ABC, a přímka Ag nechť je společnou tečnou obou křivek v bodě A a dělí úsečky DB, EC, db a ec v bodech F, G, f a g. Potom, pokud délka Ae zůstává stejná a body B a C se přibližují k bodu A; když úhel cAg mizí, křivočaré plochy Abd a Ace splývají přímočarými Afd a Age, a tak (podle lemmatu 5) budou v poměru čtverců stran Ad a Ae. Ale plochy ABD a ACE jsou stále úměrné těmto plochám, a strany AD a AE těmto stranám. Proto plochy ABD a ACE jsou mezně v poměru čtverců stran AD a AE. Což se mělo dokázat.

Lemma 10.

Dráha tělesa, které je poháněno konečnou silou, ať už je tato síla určitá a neměnná nebo se neustále zvětšuje nebo neustále zmenšuje, je na samém počátku pohybu v poměru čtverce času . [d ≈ t²]

Nechť čas představuje svislá osa a úsečky AD a AE [viz předchozí schéma] a způsobenou rychlost vodorovná osa a úsečky DB a EC; potom dráha je úměrná plochám ABD a ACE opsaná těmito úsečkami, a tak na samém počátku pohybu bude jeho dráha úměrná čtverci času, representovaného úsečkami AD a AE.  Což se mělo dokázat.

Důsledek 1. Z toho je možno snadno odvodit, že pro tělesa popisují podobné části podobných diagramů v úměrných časech jsou odchylky působené stejnými silami stejně působícími na tělesa měřené pomocí vzdáleností těles od těch bodů podobných diagramů, kterých by tato tělesa dosáhla v úměrných časech bez působení síly, odpovídají zhruba čtvercům časů, během kterých byly způsobeny.

Důsledek 2. Ale odchylky způsobené odpovídajícími silami a podobně působící na podobné části podobných těles jsou úměrné součinu síly a čtverce času.

Důsledek 3. Stejně je nutno chápat každou dráhu opsanou tělesem při působení různých sil. Ty jsou na samém počátku pohybu úměrné součinu síly a čtverci času.  [d ≈ f · t²]

Důsledek 4. A čtverce času jsou úměrné dráze a nepřímo úměrné síle. [t² ≈ x / f]

Komentář.

Když jsou nějaké veličiny různého druhu srovnávány navzájem a o kterékoliv z nich je řečeno, že je přímo nebo nepřímo úměrná druhé, znamená to, že ta prvá klesá nebo roste ve stejném nebo převráceném poměru jako ta druhá. A říkáme-li o některé, že je úměrná dvěma či více jiným, přímo nebo nepřímo, znamená to, že ta prvá roste nebo klesá v poměru, který je vypočten z poměrů, ve kterých jsou ty ostatní nebo jejich převrácené hodnoty zmenšeny nebo zvětšeny. Je-li např. řečeno, že A je přímo úměrné B a  C a nepřímo D, znamená to, že A se zmenšuje nebo zvětšuje ve stejném poměru jako , tj. A a  si jsou úměrné v daném poměru.

Lemma 11.

Pro všechny křivky mající konečnou křivost v bodě kontaktu je v mezním případě mizející délka protilehlé tětivy [subtense] kontaktního úhlu úměrná čtverci délky protilehlé tětivy [subtensi] sousedního úhlu. [b ≈ d²]

Případ 1. Nechť AB je oblouk a AD jeho tečna, BD je protilehlou tětivou [subtense] kontaktního úhlu [ BAD] kolmou k tečně a [přímka] AB protilehlou tětivou [subtense] oblouku [AB]. Sestrojme přímku BG  kolmou k tětivě AB a přímku AG  kolmou k tečně AD, které se protínají v bodě G; potom ať se body D, B a G  přibližují k bodům d, b, g; nechť J  je mezní hodnotou průsečíku BG  s  AG  když se body D a  B dostanou do bodu A. Je zřejmé, že vzdálenost GJ  může být menší, než libovolná předem daná hodnota. A dále (z podstaty kružnic procházejících body A, B, G a  a, b, g) je AB²  rovno AG × BD, a Ab² je rovno Ag × bd , a tedy poměr AB²  k Ab² je vypočten z poměrů AG  k Ag a BD  k bd. Jelikož ale vzdálenost GJ  může být udělána menším než libovolná hodnota, že poměr AG  k Ag  od se může lišit od mezní hodnoty o méně než libovolný daný rozdíl„ liší se poměr AB²  k Ab² od poměru BD  k bd  méně než libovolná daná hodnota. Proto podle lemmatu 1 je mezní poměr AB²  k Ab² stejný, jako mezní poměr BD  k bd.  Což se mělo dokázat.

Případ 2. Je-li BD je odkloněno od AD o libovolný daný úhel, bude mezní poměr BD k bd  stále stejný jako předtím a tedy stejné jako AB²  k Ab². Což se mělo dokázat.

Případ 3. Ani když úhel D není zadán, pokud se přímka BD  blíží k danému bodu nebo je sestrojena podle jiné specifikace, stále úhly D a d  (sestrojené podle společné specifikace) budu se vždy blížit k sobě a přiblíží se natolik těsně, že jejich rozdíl je možno učinit menší než libovolnou předem danou hodnota, a proto si budou podle lemmatu 1 mezně rovny; a proto úsečky BD a bd  budou ve stejném vzájemném poměru jako předtím. Což se mělo dokázat.

Důsledek 1. Jelikož tečny AD a Ad, oblouky AB a  Ab a jejich vnitřní tětivy BC a bc [sinus] jsou v mezním případě ve stejné jako tětivy AB a Ab a jejich čtverce jako vnější tětivy BD a bd. [a ~ d ~ s]

Důsledek 2. Čtverce těchto tečen, oblouků a vnitřních tětiv jsou mezně stejné jako výšky oblouků, které půlí tětivy a směřují k danému bodu. Proto jsou tyto výšky jako vnější tětivy BD a bd. [a² ~ d² ~ s² ≈ g]

Důsledek 3. A tak je tato výška úměrná čtverci času, za který těleso opíše oblouk danou rychlostí. [g ≈ t²]

Důsledek 4. Plochy přímkových trojúhelníků ADB a Adb jsou mezně v poměru třetích  mocnin stran AD a Ad  a v třípolovinovém poměru stran DB a db, jelikož plochy těchto tyto trojúhelníků jsou v poměru vypočteném z poměrů AD a DB  k Ad a db. A tak i plochy trojúhelníků ABC a Abc jsou mezně v poměru třetích mocnin stran BC a bc. Poměr který nazývám třípolovinovým je polovinou třetí mocniny, neboli vypočteného jako prvá a poloviční mocnina. [Δ ≈ g³; Δ ≈ b^3/2]

Důsledek 5. A jelikož DB a db jsou mezně rovnoběžné a v poměru druhých mocnin k AD a Ad, mezní křivočaré plochy ADB a Adb budou (podle vlastností paraboly) dvěmi třetinami přímkových trojúhelníků ADB a Adb a segmenty AB a Ab budou třetinami těch samých trojúhelníků. Proto tyto plochy a segmenty budou v poměru třetích mocnin jak k tečnám AD a Ad tak k tětivám AB a Ab a jejich obloukům.

Komentář.

Všude jsme předpokládali, že kontaktní úhel není ani nekonečně větší ani nekonečně menší než jsou kontaktní úhly, jaké mají kružnice se svými tětivami. to znamená, že křivost v bodě A není ani nekonečně malá ani nekonečně velká, tj. že vzdálenost AJ  má konečnou velikost. Potom DB  by mohlo být úměrné AD³, v takovém případě nelze sestrojit kružnici mezi tečnu AD a křivku AB, a proto kontaktní úhel bude nekonečně menší než u kružnic. Stejně je tomu, pokud by DB bylo úměrné AD⁴, AD⁵, AD⁶, AD⁷, … , potom by se řada kontaktních úhlů blížila nekonečnu, z nichž každý z nich je nekonečně menší než předchozí. Ale pokud pokládáme DB postupně za úměrné AD², AD^3/2, AD^4/3, AD^5/4, AD^6/5, AD^7/6, … , vede to k další nekonečné řady kontaktních úhlů, ze kterých prvý je stejného typu jako u kružnic, druhý nekonečně větší, a každý z následujících je nekonečně větší než ty předchozí. Kromě toho mezi každou z těchto dvojic úhlů je možno vložit nekonečnou řadu mezilehlých úhlů, ze kterých je každý nekonečně menší nebo větší než ty předchozí, např. mezi členy AD² a AD³ je možno vložit řadu AD^13/6, AD^13/6, AD^11/5, AD^9/4, AD^7/3, AD^5/2, AD^8/3, AD^11/4, AD^14/5, AD^17/6, … . A mezi libovolné členy této řady je možno vložit řadu mezilehlých úhlů, které se od sebe liší nekonečnými intervaly. Příroda nezná žádné meze.

Což bylo prokázáno o křivkách a jimi tvořených plochách je možno snadno použito na trojrozměrné křivé plochy a jejich obsah. Uvedl jsem tato lemmata před větami, abych zabránil únavnému psaní zdlouhavých důkazů sporem ve stylu starých geometrů . Ovšem důkazy je možno provádět mnohem stručnější metodou infinitezimálního počtu. Ale jelikož infinitezimálního počet není obecně přijímán a je proto pokládán za méně geometrický, dal jsem přednost uvedení důkazů metodou závislou na mezních součtech a poměrech mizejících a prvotně vznikajících hodnot, o limitách takových součtů a poměrů, a tak uvést předem co nejjasnější důkazy těchto limit. Protože těmito metodami jsou dosaženy stejné výsledky jako pomocí  infinitezimálního počtu, budeme na bezpečnějším základě použitím právě dokázaných principů. Podobně ve všem následujícím jsou veličiny brány jako sestávající z částí a kdekoliv používám prvky křivek namísto přímek, nemám na mysli infinitezimální [nekonečně malé], ale mizející dělitelné veličiny, a ne součty a poměry,a že síla těchto důkazů je vždy založena na metodách předchozích lemmat.

 Je možno namítat, že neexistuje nic takového jako mezní úměrnost mizejících veličin, jelikož před vymizením není úměrnost mezní a po vymizení neexistuje vůbec. Ale na základě stejného argumentu může být právě tak tvrzeno, že neexistuje mezní rychlost tělesa po dosažení určitého místa ve kterém pohyb ustane, jelikož před dostižením místa není rychlost mezní a po jeho dostižení už vůbec žádná neexistuje. Ale odpověď je prostá: abychom nechápali mezní rychlost jako tu, kterou se těleso pohybuje, ani před dostižením mezního místa, kde pohyb ustane, ani když je opustí, tj. právě tu rychlost,  kterou těleso dosáhne mezního místa a se kterou pohyb vymizí. A stejně poměru mizejících veličin se musí rozumět ne jako poměru veličin před jejich vymizením nebo když už vymizely, ale poměr se kterým mizejí. A podobně prvotní poměr vznikajících veličin je poměr, ve kterém vznikají. A prvotní a mezní součet se kterým začínají a přestávají existovat (nebo se zvětšovat či zmenšovat). Existuje mez, které tyto veličiny mohou dosáhnout na konci pohybu, ale nemůže být překročena. To je mezní rychlost. A stejně je tomu pro mez všech veličin a úměrností, které právě vznikají nebo zanikají. A protože tato mez je jistá a konečná, je její určení čistě geometrický problém. A vše, co je geometrické je právem používáno k určování a dokazování všeho, co může být geometrické.

Je možno též namítat, že jestliže je dána mezní poměry mizejících veličin, budu dány i jejich mezní hodnoty, a tak každá hodnota bude sestávat z infinitezimálních veličin, což je v rozporu s tím, co dokázal Euklides o nesrovnatelnosti v desáté knize svých Základů. Ale tato námitka je založena na špatné hypotéze. Ty mezní poměry, se kterými veličiny mizí, nejsou skutečné poměry mezních hodnot, ale mez, ke které se poměry veličin neomezeně klesajících blíží a ke kterému se může přiblížit tak těsně, že jejich rozdíl je menší než libovolná daná hodnota, ale kterou nemohou nikdy přesáhnout ani dosáhnout, dokud veličiny nevymizí nekonečně. Podstata věci bude srozumitelná jasněji v případě veličin, které jsou nekonečně velké. Jestliže se dvě veličiny, jejichž rozdíl je pevně dán, nekonečně rostou, jejich mezní poměr je znám, totiž poměr rovnosti, ale z toho nevyplývá, že budou známy mezní nebo největší hodnoty, jejichž poměr se jedná. Proto tedy, jestliže v následujícím textu, aby byl srozumitelnější, pokusím se zmiňovat co nejméně o těchto veličinách, ať už mizejících nebo mezních, a nebudete nuceni se domnívat, že jsou míněny jakékoliv určité hodnoty, ale vždy jsou myšleny veličiny, které nekonečně klesají.

Sekce 2.

O nalezení centrálních sil .

Tvrzení 1.  Věta 1.

Plochy které opisují při pohybu tělesa po oběžné dráze průvodiče, které je spojují s nepohyblivým centrem sil, leží v pevných rovinách a jsou úměrné času. . [Φ ≈ t]

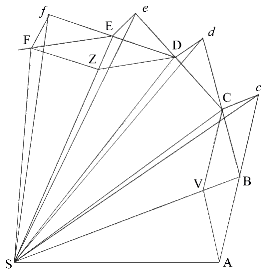Rozdělme čas na stejné části, a v prvé části času nechť těleso svou setrvačností opíše úsečku AB. V druhé části času, pokud mu v tom nebude nic bránit, bude toto těleso opisovat (podle zákona 1) přímku do bodu c a opíše dráhu Bc rovnou AB, takže když doplníme spojnice se středem AS, BS a cS, opsalo by stejnou plochu ASB a BSc. Ale když těleso dojde do B, nechť centrální síla zapůsobí krátkým silným impulsem a odchýlí ho a způsobí odchýlení tělesa od přímky Bc do přímky BC. Nechť cC je rovnoběžná s BS a protne přímku BC v bodě C; potom, když skončí druhá část času, bude se těleso nacházet (podle důsledku 1 zákonů) v bodě C ve stejné rovině jako trojúhelník ASB. Propojíme SC, a protože SB a Cc jsou rovnoběžné, trojúhelník SBC bude stejný jako trojúhelník SBc, a tedy i trojúhelníku SAB. Podle stejných argumentů, pokud centrální síla působí postupně v bodech C, D, E, … , způsobí, že těleso v jednotlivých částech času opíše jednotlivé úsečky CD, DE, EF, … , všechny v jedné rovině, a trojúhelník SCD bude roven SBC, dále SDE bude roven SCD, SEF bude roven SDE. Proto jsou v pevné rovině za stejnou dobu budou opsány stejné plochy. A po složení bude každý ze součtů SADS a SAFS těchto ploch vůči sobě v poměru doby oběhu. Nyní nechť počet trojúhelníků roste a jejich šířky se nekonečně zmenšují a jejich mezní ohraničení ADF bude (podle lemmatu 3, důsledku 4) křivka a centrální síla, která těleso stále táhne zpět od tečny této křivky, bude působit nepřerušovaně, zatímco libovolné opsané plochy SADS a SAFS, které jsou vždy úměrné době pohybu, budou v tomto případě úměrné času. Což se mělo dokázat.

 Důsledek 1. V prostoru bez odporu prostředí je rychlost tělesa přitahovaného k nehybnému středu v opačném poměru než kolmice spuštěná z tohoto středu na přímku, která je tečnou dráhy. Neboť rychlosti v bodech A, B, C, D a  E jsou základnami stejných trojúhelníků AB, BC, CD, DE a EF, a ty jsou nepřímo úměrné kolmicím na ně spuštěným . [f ≈ 1 / y]

Důsledek 2. Pokud tětivy AB a BC dvou obloků postupně opsaných stejným tělesem v prostoru bez odporu prostředí jsou doplněny na rovnoběžník ABCV, potom když diagonála BV (v posici, kterou má mezně když tyto úhly mizí) protažena na obě strany bude procházet středem sil.

Důsledek 3. Když jsou tětivy AB, BC a DE, EF  oblouků opsaných za stejný čas v prostoru bez odporu prostředí doplněny na rovnoběžníky ABCV a DEFZ, potom síly v bodech B a E jsou navzájem v mezním poměru diagonál BV a EZ  když se oblouky nekonečně zkracují. Jelikož pohyby BC a EF jsou (podle důsledku 1 zákonů) složeny z pohybů Bc, BV a Ef, EZ a jelikož BV a EZ jsou stejné jako Cc a Ff, které byly vyvolány impulsy centrální síly v bodech B a E, a proto jsou úměrné těmto impulsům.

Důsledek 4. Síly kterými jsou tělesa v prostoru bez odporu tažena od přímočarého pohybu na křivočaré dráhy jsou ve vzájemném poměru jako výšky oblouků opsaných za stejnou dobu, které míří k centru sil a dělí na polovinu tětivy když se úhly nekonečně zmenšují. Protože tyto výšky jsou polovinou diagonál rozebíraných v důsledku 3. [f ≈ g]

Důsledek 5. To vše platí podle důsledku 5 zákonů, když roviny, ve kterých se tělesa pohybují spolu s centrem sil v týchž rovinách, nejsou v klidu ale pohybují se rovnoměrně přímočaře.

Tvrzení 2.  Věta 2.

Každé těleso, které se pohybuje po rovinné křivce a jeho průvodič, který ho spojuje s bodem, který se buď nepohybuje nebo se pohybuje rovnoměrně přímočaře, opisuje okolo tohoto bodu plochy úměrné časům, je vychylován centrální silou směřující k tomu samému bodu..

Případ 1. Neboť každé těleso, které se pohybuje po nějaké rovinné křivce je vychylován z přímočarého pohybu nějakou silou, která na něj působí (podle zákona 1). A taková síla, kterou je těleso vychylováno z přímočaré dráhy a za stejný čas způsobí, že opíše za stejné časy okolo nehybného bodu S stejné malé trojúhelníky SAB, SBC, SCD, … působí v bodě B podél přímky rovnoběžné k cC (podle tvrzení 40 knihy 1 Euklidových Základů. a zákona 2), tj. podle přímky BS,a v bodě C působí síla podle přímky rovnoběžné s dD, tj. podle přímky SC, … . Tedy působí stále podle přímek směřujících do tohoto nepohyblivého bodu S. Což se mělo dokázat.

 Případ 2. A podle důsledku 5 zákonů není rozdílu, zda plocha po které těleso koná křivočarou dráhu je v klidu nebo se pohybuje rovnoměrně přímočaře vpřed spolu s tělesem, opisovanou křivkou a s bodem S.

Důsledek 1. V prostorech  nekladoucích odpor, pokud plochy nejsou úměrné času, síly nesměřují k bodu kde se poloměry protínají ale odklánějí se od něho vpřed, tj. ve směru, ke kterém těleso směřuje a působí, že plochy se zrychlují; ale pokud je zpožděný, odchylují se dozadu.

Důsledek 2. I v mediích kladoucích odpor, pokud se opisované plochy zrychlují, směry těchto sil se odchylují od bodu, kde se poloměry protínají, ve směry pohybu.

Komentář

 Těleso může být vychylováno centrální silou složenou s několika složek. V tom případě je význam tvrzení takový, že síla která je složením všech těchto sil směřuje k bodu S. Dále, pokud některá síla působí stále podél přímky kolmé k popsané ploše, způsobí, že těleso se odchýlí z roviny pohybu, ale nikdy nezvýší nebo nezmenší  velikost popsané povrchové plochy a musí proto být ignorována ve složené síle.

Tvrzení 3.  Věta 3.

Na každé těleso, které svým průvodičem, který ho spojuje se středem jiného tělesa, které se libovolně pohybuje, opisuje kolem tohoto středu plochy úměrné času působí síla, která je složená z centrální síly mířící k druhému tělesu a ze zrychlující síly jaká působí na druhé těleso .

Označme prvé těleso L a druhé těleso T; a pokud je (podle důsledku 6 zákonů) na každé z těles působeno podle rovnoběžek novou silou, která je stejná a opačná síle, která působí na těleso T, těleso L bude nadále opisovat kolem tělesa T stejné plochy jako dříve, ale síla působící na těleso T bude rušena stejnou silou opačného směru, a proto (podle zákona 1) těleso T  zůstane samo o sobě buď v klidu nebo se bude pohybovat rovnoměrně přímočaře, a těleso L bude vzhledem k rozdílu sil, které na něj působí, dále opisovat plochy úměrné času kolem tělesa T. Proto rozdíl sil směřuje k druhému tělesu jako centru. Což se mělo dokázat.

Důsledek 1. A tedy, když těleso L svým průvodičem k jinému tělesu T  opisuje plochy úměrné času, a z celkové zrychlující síly (ať už jednoduché nebo složené z několika sil podle důsledku 2 zákonů) působící na těleso L je odečtena (podle téhož důsledku zákonů) celková zrychlující síla působící na těleso T, potom zbytková síla která na těleso L působí bude mířit k tělesu T jako středu.

Důsledek 2. I když jsou ty plochy jen přibližně úměrné času, zbytková síla bude mířit k tělesu T  jen přibližně.

Důsledek 3. A naopak, jestliže zbytková síla směřuje jen přibližně k tělesu T, plochy budou jen přibližně úměrné časům.

Důsledek 4. Pokud průvodič tělesa L, který ho spojuje s jiným tělesem T, opisuje plochy, které jsou  ve srovnání s časem velmi nestejné a těleso T je v klidu nebo se pohybuje rovnoměrně přímočaře, buď neexistuje centrální síla směřující k tělesu T nebo je působení centrální síly smíšeno a složeno se silným působením jiných sil a celková síla po složení všech sil, pokud je jich několik, směřuje k jinému středu (pevnému nebo pohyblivému). Totéž platí, pokud se druhé těleso pohybuje jakýmkoliv jiným pohybem, pokud za centrální sílu bereme to, co zbude po odečtení celkové síly působící na druhé těleso T.

Komentář

Jelikož stejnoměrné opisování plochy označuje ten střed, jehož síla je ta, která těleso nejvíce ovlivňuje a která ho odklání od přímočarého pohybu a udržuje na oběžné dráze, proč bychom nemohli v dalším využít stejnoměrné opisování ploch jako kritérium toho středu, okolo kterého probíhá veškerý orbitální pohyb ve volném prostoru ?

Tvrzení 4.  Věta 4.

 Centrální síly těles, která opisují kružnice rovnoměrným pohybem míří ke středům těchto kružnic a jsou ve vzájemném poměru jako čtverce ploch opsaných za stejný čas dělené poloměry kružnic . 

Tyto síly směřují ke středům kruhů podle tvrzení 2 a důsledku 2 tvrzení 1, a jsou vůči sobě jako převrácené siny oblouků opsaných za malé rovné časy podle důsledku 4 tvrzení 1, a čtverce těchto oblouků dělených poloměry kruhů podle lemy 7, a proto, jelikož tyto oblouky jsou stejné jako oblouky opsané za libovolný stejný čas a průměry jsou jak jejich poloměry, síly budou jako čtverce libovolných oblouků opsaných za stejný čas dělených poloměrem kruhů. Což se mělo dokázat.

Důsledek 1. Jelikož  tyto oblouky jsou ve stejném poměru jako rychlosti těles, jsou centrální síly úměrné poměru vypočtenému ze čtverce rychlostí a převrácené hodnoty poloměru. [f ≈ v² / r]

Důsledek 2. A protože oběžné doby jsou v poměru vypočteném z přímého poměru poloměrů a převráceného poměru rychlostí, jsou centrální síly v poměru vypočteném z přímého poměru poloměrů a čtverce převráceného poměru oběžných dob. [f ≈ r / T²]

Důsledek 3. Proto, pokud jsou oběžné doby stejné a tedy rychlosti jsou úměrné poloměrům, centrální síly budou také v poměru poloměrů a naopak.

Důsledek 4. Jestliže jak oběžné doby tak rychlosti jsou v poměru odmocnin poloměrů, potom si budou centrální síly rovné a naopak.

Důsledek 5. Pokud jsou oběžné doby úměrné poloměrům a rychlosti jsou proto stejné, centrální síly budou v převráceném poměru poloměrů, a naopak.

Důsledek 6. Pokud jsou běžné doby jako 3/2 mocnina poloměru a tedy rychlosti jsou úměrné odmocnině poloměru, centrální síly budou úměrné převrácenému poměru čtverců poloměrů, a naopak.

Důsledek 7. A obecně, pokud jsou oběžné doby ve stejném poměru jako mocnina Rⁿ poloměru R, a tedy rychlosti jsou v opačném poměru než  R ^n-1 poloměru a centrální síly budou v opačném poměru než R ^2n-1 poloměru a naopak.

Důsledek 8. V případech, kdy tělesa opisují podobné části libovolných obrazců, které jsou podobné a mají podobně umístění středy v těchto obrazcích, stejné úměry vzhledem k času, rychlostem a silám, jak vyplývá z aplikace předchozích důkazů pro tyto případy. Taková aplikace vznikne záměnou rovnoměrného opisování ploch za rovnoměrný pohyb a záměnou vzdáleností bodů od středu za poloměr.

Důsledek 9. Ze stejných důkazů vyplývá, že oblouk, který opíše za stejný čas těleso, které se rovnoměrně pohybuje po kružnici s danou centrální silou, je geometrickým průměrem mezi průměrem kružnice a dráhou, kterou by těleso spadlo působením stejné síly za stejný čas .

Komentář

Případ důsledku 6 platí pro těžká tělesa (jak nezávisle zjistili naši kolegové Wren, Hooke a Halley). Pro jsem usoudil, že to následující by mělo pojednávat spíše o otázkách spojených s centrálními silami které klesají se čtvercem vzdálenosti.

Kromě toho s pomocí předchozích tvrzení a jejich důsledků může být též určena úměrnost centrálních sil, jako je gravitace. Jelikož jestliže těleso obíhá působením síly v kruzích s centrem v Zemi, tato přitažlivost je centrální silou. Navíc, za základě důsledku 9 tvrzení 4 je jak doba oběhu a oblouk opsaný za daný čas jsou známy s pádu těžkých těles. A na základě tvrzení podobného typu Huygens ve svém výtečném díle O kyvadlových hodinách  srovnává sílu gravitace s centrální silou točících se těles.

Toto tvrzení je též možno demonstrovat následujícím způsobem. V libovolném kruhu předpokládejme vepsaný mnohoúhelník s libovolným počtem stran. A pokud se těleso pohybuje s danou rychlostí podél stran mnohoúhelníku, pružně se odrazí od kruhu v každém úhlu mnohoúhelníku a síla se kterou narazí na kruh při každém odrazu bude úměrná rychlosti, a proto součet sil v daném okamžiku bude úměrný součinu rychlosti a počtu odrazů, tj. (jsou-li určeny strany a úhly mnohoúhelníku) délce opsané za daný čas zvětšený nebo zmenšený v poměru délky oblouku k poloměru zmíněného kruhu, tj. čtverci této délky dělené poloměrem. A když se potom strany nekonečně zmenší, mnohoúhelník splyne s kruhem a součet sil v daném čase bude úměrná čtverci opsaného oblouku opsaného za daný čas děleného poloměrem. Je to odstředivá síla kterou těleso působí na kruh, a opačná síla, kterou kruh neustále zahání těleso ke středu, je rovna odstředivé síle.

Tvrzení 5.  Problém 1.

 V libovolném bodě je dána rychlost kterou těleso opisuje danou křivku když na něj působí síly mířící k  nějakému společnému středu, najít tu sílu .

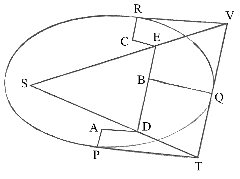Nechť se takto popsané křivky dotýkají ve třech bodech P, Q a R tři přímky PT, TQV a VR, které se protínají v bodech T a V. Sestrojme úsečky PA, QB a RC kolmé k tečnám a nepřímo úměrné rychlostem tělesa v bodech P, Q a R, z nichž jsou kolmice sestrojeny, tj. PA je k QB ve stejném poměru jako rychlost  v bodě Q k rychlosti v bodě P a QB k RC jako  rychlost v bodě R k rychlosti v bodě Q. Na konci A, B a C kolmic  sestrojme AD, DBE a EC v pravých úhlech k těmto kolmicím, nechť se protnou v bodech D a E; potom RD a VE se po prodloužení protnou v hledaném středu S.

Jelikož kolmice spuštěné ze středu S k tečnám, PT a QT jsou (podle důsledku 1 tvrzení 1) v opačném poměru k rychlostem tělesa v bodech P a Q a tedy podle konstrukce k AP a BQ ve stejném poměru, tj. jako kolmice spuštěná z bodu D na tečnu. Z toho je možno snadno odvodit, že body S, D a T leží na jedné přímce, a proto  střed S je průsečíkem přímek TD a VE. Což se mělo dokázat.

Tvrzení 6.  Věta 5.

 Jestliže v prostoru bez odporu těleso obíhá po kolem nehybného středu a opisuje právě vznikající oblouk v nekonečně krátkém čase, a jestliže výška oblouku je chápána tak, že dělí na poloviny tětivu oblouku a při prodloužení prochází středem sil, potom je centrální síla uprostřed oblouku v přímém poměru k výšce a nepřímo ke čtverci času . [f ≈ g / t²]

Jelikož výška je v daném čase úměrná síle (důsledek 4 tvrzení 1) a jestliže čas vzroste v nějakém poměru, potom, potom oblouk vzroste ve stejném poměru, výška vzroste v poměru čtverce času (důsledek 2 a 3 lemmatu 11) a tedy je úměrná síle a čtverci času. Vydělme obě strany čtvercem času, síla bude přímo úměrná výšce a nepřímo čtverci času . Což se mělo dokázat.

Toto tvrzení je též jednoduše dokázáno důsledkem 4 lemmatu 10.

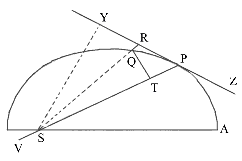Důsledek 1. Pokud těleso P obíhající okolo středu S opisuje křivku APQ a tečna ZPR se té křivky dotýká v bodě P, z libovolného bodu Q křivky je spuštěna na tečnu úsečka RQ rovnoběžná s průvodičem SP, která protíná tečnu v bodě R a dále úsečka QT kolmá k průvodiči SP, potom je centrální síla úměrná výrazu za předpokladu, že velikost tohoto výrazu je vzata jako mezní hodnota když body P a  Q se přibližují. Jelikož QR je rovno výšce oblouku, která je rovna dvojnásobku oblouku QP s bodem P uprostřed a zdvojuje trojúhelník SQP o ploše SP × QT úměrné času, za který je tento dvojnásobný oblouk opsán a tedy může být použit namísto času.

Důsledek 2. Podle stejných argumentů je centrální síla nepřímo úměrná výrazu ,  kde SY je kolmice spuštěná ze středu sil na tečnu PR dráhy. Neboť SY × QP a  SP × QT jsou obsahy téhož trojúhelníku [SRP].

Důsledek 3. Pokud dráha APQ je buď kruhová nebo se dotýká kruhu soustředně nebo ho soustředně protíná, tj. má s kruhem nejmenší možný úhel kontaktu nebo průsečíku a má stejnou křivost a stejný poloměr křivosti v bodě P a když PV je tětiva kruhu vedoucí od tělesa středem sil, potom centrální síla v opačném poměru než výraz SY² × PV. Neboť PV je rovno .

Důsledek 4. Z a stejných podmínek je centrální síla přímo úměrná čtverci rychlosti a nepřímo úměrná tětivě. Neboť rychlost je nepřímo úměrná kolmici SY podle důsledku 1 tvrzení 1. [f ≈ v² / d]

Důsledek 5. Proto, je-li dána křivočarý diagram APQ a je dán střed S, k němuž centrální síly neustále směřují, je možno najít zákon pro centrální sílu, podle kterého je těleso P odkláněno z přímočaré dráhy a je drženo na průvodiči tohoto diagramu a obíhat po oběžné dráze. Je nutno vypočítat výraz nebo výraz SY² × PV  nepřímo úměrné této síle. Příklady budou uvedeny v příštích problémech.

Tvrzení 7.  Problém 2.

 Nechť se těleso pohybuje po obvodu kruhu; najít zákon centrální síly směřující k danému bodu .

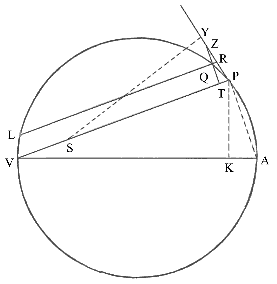Nechť VQPA je obvod kruhu, S daný bod, ke kterému míří síla jako ke středu, P těleso obíhající po kruhu, Q jeho příští poloha, PRZ tečna kruhu v bodě P. Středem S veďme tětivu kruhu PV, a po doplnění průměru VA spojme AP a na průvodič SP spusťme kolmici QT, která protne tečnu PR v bodě Z; a nakonec bodem Q sestrojme tětivu LR rovnoběžnou s  SP, která protne kruh v bodě L a tečnu PZ v bodě R. Jelikož trojúhelníky ZQR, ZTP a  VPA jsou shodné, bude RP² (rovné QR × RL )  k QT² jako AV² k  PV². A tedy je rovno QT². Vynásobme tyto stejné výrazy , a jelikož se body P a  Q přibližují, dosadíme PV místo RL. Potom bude rovno . Proto (důsledky 1 a 5 tvrzení 6) je centrální síla v opačném poměru než , tj. (protože AV² je pevné) v opačném poměru než součin čtverce vzdálenosti od středu SP a třetí mocniny tětivy PV. Což se mělo zjistit.

Jiné řešení

Sestrojme SY kolmou k prodloužené tečně PR; potom, jelikož trojúhelníky SYP a  VPA jsou podobné, AV bude k  PV jako SP k  SY, a tedy bude rovno SY, a bude rovno SY² × PV. A tedy (důsledky 3 a 5 tvrzení 6) centrální síla bude v opačném poměru než , a jelikož AV je pevné, v opačném poměru než SP² × PV³. Což se mělo zjistit.

Důsledek 1. Proto, je-li dán bod S ke kterému stále směřuje centrální síla na obvodu kruhu, řekněme v bodě V, tato centrální síla bude v opačném poměru než pátá mocnina vzdálenosti SP.

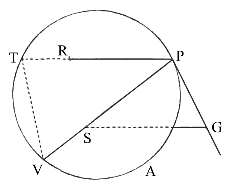Důsledek 2. Síla, jejímž působením těleso P obíhá po kruhu APTV  kolem centra sil S je k síle, jejímž působením by stejné těleso P obíhalo se stejnou dobou oběhu kolem libovolného jiného středu sil R jako RP² × SP ke třetí mocnině úsečky SG, která je spuštěna z prvého středu sil S na tečnu dráhy PG a je rovnoběžná se vzdáleností tělesa od druhého středu sil. Neboť podle konstrukce tohoto tvrzení je prvá síla ke druhé síle ve stejném poměru jako RP² × PT³, tj. jako SP × RP² k , a tedy (protože trojúhelníky PSG a TPV jsou podobné) jako SG³.

Důsledek 3. Síla, jejímž působením těleso P obíhá po libovolné dráze kolem centra sil S je k síle, kterou by stejné těleso P obíhalo po stejné dráze se stejnou dobou oběhu kolem jiného středu sil R je jako výraz SP × RP², složený ze vzdálenosti od prvého středu S a čtverce vzdálenosti od druhého středu R, ke třetí mocnině úsečky SG, která je spuštěna z prvého středu sil na tečnu dráhy PG a je rovnoběžná se vzdáleností RP tělesa od druhého středu sil. Jelikož síly na této dráze  v libovolném bodě P jsou stejné, jako v případě kružnice se stejnou křivostí.

Tvrzení 8.  Problém 3.

Nechť se těleso pohybuje po polokruhu  PQA; najít zákon centrální síly pro ten případ, kdy centrální síla míří k bodu S tak vzdálenému, že všechny přímky  PS a  RS, které k němu směřují, je možno pokládat za rovnoběžné .

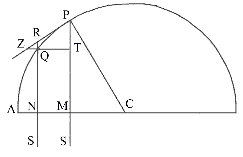Ze středu C polokruhu sestrojíme poloměr CA, protínající příslušné rovnoběžky kolmo v bodech M a N, a propojme CP. Protože trojúhelníky CPM, PZT a  RZQ jsou podobné, je CP² k  PM² jako PR² k  QT², a z podstaty kruhu je PR² rovno obdélníku QR × (RN + QN) , a protože body P a  Q se přibližují, obdélníku QR × 2·PM. Tedy CP² je k  PM² jako QR × 2·PM  k  QT², a tedy je rovno . A tedy (podle důsledku 1 a 5 tvrzení 6) je centrální síla v opačném poměru jako , to je ( po vynechání pevného výrazu ) v obráceném poměru než PM³. Což se mělo zjistit.

Komentář

A na základě nepříliš odlišného argumentu, pro těleso pohybující se po elipse nebo dokonce po hyperbole či parabole působením centrální síly, že je v obráceném poměru ke třetí mocnině výšky, když síla působí směrem k velmi vzdálenému středu.

Tvrzení 9.  Problém 4.

Nechť se těleso pohybuje po spirále PQS a protíná všechny její poloměry Sp, Sq, … pod pevným úhlem; najít zákon centrální síly směřující do směru spirály .

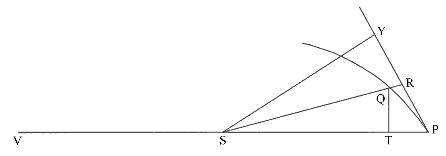Nechť je dán nekonečně malý úhel PSQ. Protože všechny úhly jsou dané, jsou dány i všechny poměry částí diagramu SPRQT. Proto poměr je pevný a je ve stejném poměru jako QT, tj. (protože poměry částí diagramu jsou pevné) jako SP. Nyní změňme úhel PSQ takovým způsobem, aby se přímka QR přepínající kontaktní úhel QPR změnila (podle lemmatu 11) jako čtverec PR nebo QT. A tedy zůstane stejné jako předtím, tedy jako SP. A tedy je jako SP², a tedy (důsledky 1 a 5 tvrzení 6) centrální síla je v opačném poměru než vzdálenost SP. Což se mělo zjistit.

Jiné řešení

Kolmice SY spuštěná na tečnu a tětiva PV kružnice kružnice protínající spirálu soustředně mají ke vzdálenosti SP pevné poměry, a tak SP³ je jako SY² × PV, tj. (pdle důsledků 3 a 5 tvrzení 6) nepřímo úměrné centrální síle.

Lemma 12.

Všechny rovnoběžníky sestrojené nad libovolnými sdruženými průměry dané elipsy nebo hyperboly jsou navzájem rovné .

Vyplývá to z vlastností kuželoseček.

Tvrzení 10.  Problém 5.

Nechť těleso obíhá po elipse; najít zákon centrální síly směřující ke středu elipsy . 

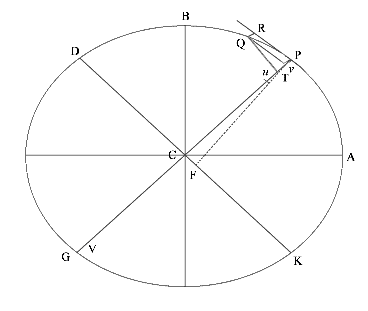Nechť CA a CB jsou poloosy elipsy, GP a DK jiné sdružené průměry, PF a QT  kolmice k těmto průměrům a Qv výška vztažená k průměru GP; po doplnění rovnoběžníku QvPR bude obdélník Pv × vG (na základě vlastností kuželoseček) ke Qv² jako PC²  k CD², a (protože trojúhelníky QvT a PCF jsou podobné) Qv² je k QT² jako PC²  k PF² , a po kombinaci těchto poměrů je obdélník Pv × vG  k QT² jako PC² k CD² a PC² k PF², tj.vG je k  vve stejném poměru jako PC² k . Nahraďme QR místo Pv a (podle lemmatu 12) BC × CA  místo CD × PF, a též (protože body P a Q se sbližují) 2·PC namísto vG a po roznásobení a dosazení mezních hodnot se stává rovným . A tedy (podle důsledku 5 tvrzení 6) je centrální síla v opačném poměru než , tedy (jelikož 2·BC² × CA² je pevné) v opačném poměru než , jt v přímém poměru jako vzdálenost PC. Což se mělo zjistit.

Jiné řešení

Na přímce PG zvolme bod u  na druhé straně od bodu T tak, aby platilo Tu je rovno Tv, potom zvolme V tak, aby platilo , že je k vG ve stejném poměru jako DC² k PC². A jelikož (podle vlastností kuželoseček) platí, že Qv² je k Pv × vG jako DC² k PC², bude Qv² rovno Pv × uV. Přidejme k oběma stranám obdélník uP × pV, a čtverec tětivy úhlu PQ se stává rovným obdélníku  VP × Pv; a tedy se kružnice, která se dotýká kuželosečky v bodě P a prochází bodem Q bude též procházet bodem V. Nech't se body P a Q přibližují a poměr uV k vG, který je stejný jako poměr DC² k PC², se stane poměrem PV nebp PG k 2·PC, a tedy PV bude rovno . Díky tomu síla, pod jejímž vlivem těleso P obíhá po elipse bude (podle důsledku 3 tvrzení 6) v opačném poměru než a tedy (protože 2·DC² × PF² je pevné) jako PC. Což se mělo zjistit.

Důsledek 1. Proto je síla úměrná vzdálenosti tělesa od středu elipsy, a naopak, pokud je síla úměrná vzdálenosti, těleso bude obíhat po elipse se středem v centru sil, případně bude obíhat po kruhu, ve který se elipsa promění.

Důsledek 2. A doby oběhu  po elipsách obecně kolem jejich středu si budou rovné. Pro podobné elipsy jsou si časy rovné (podle důsledků 3 a 8, tvrzení 4) zatímco elipsy se společnou hlavní osou jsou ve vzájemném poměru jako celková plocha elips a v opačném poměru než části ploch opsané průvodičem za stejný čas, to znamená přímo úměrné vedlejším osám a nepřímo úměrné rychlosti těles na hlavních vrcholech nepřímo, tj. přímo těmto vedlejším osám a nepřímo vzdálenosti téhož bodu od hlavní osy,a proto (vzhledem k rovnosti přímého a nepřímého poměru) ve stejném poměru.

Komentář

Když se střed elipsy vzdaluje do nekonečna, elipsa se mění v parabolu a síla mířící k nekonečně vzdálenému středu je stále stejná. To je Galileiho teorém. A pokud (změnou sklonu roviny sekající kužel) se parabolická kuželosečka změní na hyperbolu, těleso se bude pohybovat po obvodu hyperboly a centrální síla se změní na odstředivou sílu. A stejně jako u kruhu a elipsy,  pokud síly směřují ke středu diagramu umístěného na prvé ose, a jestliže se druhé souřadnice budou zvětšovat či zmenšovat v daném poměru a dokonce jestliže se odchylka od prvé osy změní„ sílu se stále zvětšují či zmenšují  v poměru vzdálenosti od středu, pokud se doba oběhu nemění; a obecně pro všechny diagramy, pokud se odchylky budou zmenšovat či zvětšovat v daném poměru nebo se úhel odchylky změní libovolným způsobem, pokud oběžné doby zůstávají stejné, potom se síly směřující ke středu umístěném na prvé ose pro každou jednotlivou souřadnici zvětšují či zmenšují v poměru vzdáleností od středu.

Sekce 3.

O pohybu těles po výstředných kuželosečkách .

Tvrzení 11.  Problém 6.

Nechť těleso obíhá po elipse; najít zákon centrální síly směřující k ohnisku elipsy . 

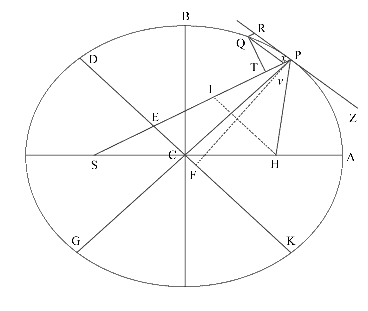Nechť S je ohnisko elipsy. Sestrojíme průvodič SP  protínající jak průměr DK elipsy v bodě E , tak úsečku Qv  v bodě x, a doplníme rovnoběžník QxPR. Je zřejmé, že EP je rovné hlavní poloose AC, protože když sestrojíme úsečku HI  rovnoběžnou s EC  z druhého ohniska H  elipsy, potom ES a  HI jsou stejné, protože CS a CH jsou stejné, a tedy EP je polovinou součtu PS a PI, tj. (jelikož HI a PR jsou rovnoběžné a úhly IPR a HPS jsou stejné) polovině součtu PS a PH (což je rovno celé ose 2·AC). Spustíme přímku QT  kolmou k SP, a jestliže L označuje hlavní latus rektum elipsy (rovný ), potom L × QR bude k  L × Pv jako QR ku Pv, tj. jako PE nebo AC k PC, a  L × Pv bude k  Gv × vP jako L ku Gv a  Gv × vP bude k  Qv² jako PC² k  CD², a tedy (podle důsledku 2 lemmatu 7) budou Qv² a  Qx² stejné, když se budou body P a  Q přibližovat a tedy Qx² nebo Qv² je ke QT² jako EP² k  PF², tj. jako CA² k  PF², nebo (podle lemmatu 12) jako CD² k  CB². A když všechny tyto poměry zkombinujeme, dostaneme L × QR bude k  QT² jako AC × L × PC² × CD², nebo jako 2·CB² × PC² × CD² k  PC × Gv × CD² × CB², neboli jako 2·PC ke Gv. Ale když se body Q a  P  přibližují, jsou 2·PC a Gv stejné. Proto L × QR a  QT², které jsou jim úměrné, jsou si též rovny. Po vynásobení rovnice , a  L × SP² se změní na . Proto (podle důsledku 1 a 5 tvrzení 6) je centrální síla nepřímo úměrná L × SP², a tedy nepřímo úměrní čtverci vzdálenosti SP. Což se mělo zjistit.

Jiné řešení

Síla, která směřuje ke středu elipsy a jejímž působením může těleso P  obíhat po této elipse, je úměrná (podle důsledku 1 tvrzení 10) vzdálenosti SP od středu elipsy; a tedy, když sestrojíme přímku CE rovnoběžnou s tečnou PR elipsy a  CE a  PS se protnou v bodě E, potom síla jejímž působením může stejné těleso P obíhat kolem kteréhokoliv jiného bodu S elipsy bude (podle důsledku 3 tvrzení 7) jako ; tedy pokud je bod S ohniskem elipsy a tedy PE je pevné, nepřímo úměrná čtverci vzdálenosti SP. Což se mělo zjistit.

Toto řešení je možno rozšířit na parabolu a hyperbolu stejně lapidárně jako u tvrzení 10, ale vzhledem k důležitosti tohoto problému a jeho používání v dalším textu nebude příliš obtížné potvrdit každý z těchto případů samostatným důkazem.

Tvrzení 12.  Problém 7.

Nechť těleso obíhá po hyperbole; najít zákon centrální síly směřující k ohnisku diagramu  . 

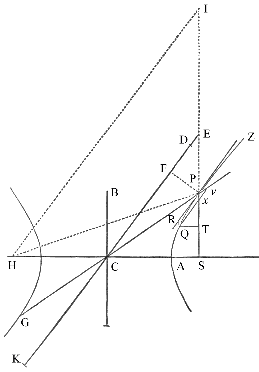Nechť CA a CB jsou poloosy hyperboly, PG a KD jiné sdružené průměry, PF  kolmice kolmice k průměru KD a Qv  úsečka k průměru GP. Sestrojíme SP protínající průměr DK v bodě E a úsečku Qv v bodě x a doplníme rovnoběžník QRPx. Je zřejmé, že EP je rovno příčné poloose AC, protože když sestrojíme přímku HI rovnoběžnou s EC z druhého ohniska H  hyperboly, ES a EI jsou stejné protože CS a CH jsou stejné, a tedy EP je rovno polovině rozdílu úseků PS a PI, a rovněž (protože IH a PR jsou rovnoběžné a úhly IPR a HPZ jsou stejné) úseků PS a PH, rozdílu, který je roven celé ose 2·AC. Spustíme QT kolmou na SP. Potom, jestliže L označuje hlavní latus rektum [viz poznámku ] hyperboly (rovný ), L × QR bude k L × Pv jako R to Pv, nebo Px k Pv, tj. (protože trojúhelníky Pxv a PEC jsou podobné) jako PE  k PC, nebo též AC k PC. Ale L × Pv bude též k Gv × Pv jako L k Pv, a (z podstaty kuželoseček [Viz poznámku ]) obdélník Gv × vP bude k Qv² jako PC² k CD², a dále (podle důsledku 2 lemmatu 7) jako poměr Qv² k Qx²; když se body P a Q přibližují, stává se rovností; a Qx² nebo Qv² je k AT² ve stejném poměru jako EP² k PF², tj. jako CA² k PF². nebo (podle lemmatu 12) jako CD² k CB², a když všechny tyto poměry zkombinujeme, potom L × QR bude ku QT² jako AC × L × PC² × CD² nebo 2·CB² × PC² × CD² k PC × Gv × CD² × CB², nebo jako 2·PC ku Gv. Když se ale body P a Q přibližují, 2·PC a Gv jsou si rovné. Proto i L × QR a QT², které jsou jim úměrné, jsou si též rovné. Vynásobme tyto rovnosti , a L × SP² se stane rovným . Tedy (podle důsledků 1 a 5 tvrzení 6) jsou centrální síly nepřímo úměrné  L × SP², a tedy nepřímo úměrní čtverci vzdálenosti SP. Což se mělo zjistit.

Jiné řešení

Najdeme sílu, která směřuje  ze středu hyperboly. Ta vychází úměrná vzdálenosti CP. A tedy (podle důsledku 3 lemmatu 7) síla směřující k ohnisku S bude jako , tj., jelikož PE je pevné, nepřímo úměrná SP². Což se mělo zjistit.

Dá se ověřit stejnou cestou, že když se přitažlivá síla změní v odpudivou, těleso se bude pohybovat po druhé větvi hyperboly.

Lemma 13.

U paraboly je latus rektum odpovídající vrcholu čtyřnásobkem vzdálenosti tohoto vrcholu od jejího ohniska .

Vyplývá to z vlastností kuželoseček [Viz poznámku ].

Lemma 14.

Kolmice spuštěná z ohniska paraboly na její tečnu je geometrickým průměrem mezi vzdáleností ohniska od bodu kontaktu a vzdálenosti vrcholu od jejího ohniska .

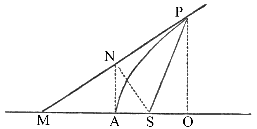Nechť AP je parabola, S její ohnisko, A hlavní vrchol, P  bod dotyku, PO kolmice k hlavnímu průměru, PM tečna protínající  hlavní průměr v bodě M  a SN  kolmice spuštěná z ohniska na tečnu. Spojme AN, a protože dvojice MS a SP, MN a  NP a MA a AO jsou stejné, přímky AN a OP  budou rovnoběžné. A jelikož trojúhelník SAN bude mít pravý úhel ve vrcholu A a totéž platí pro podobné trojúhelníky SNM a SNP, platí, že PS je ku SN jako SN  k SA. Což se mělo dokázat.

Důsledek 1. PS² je ku SN² jako PS k PA.

Důsledek 2. A protože SA je pevné, je SN² jako PS.

Důsledek 3. A bod, kde libovolná tečna PM  protíná přímku SN, která je spuštěna z ohniska kolmo na tečnu, padne na přímku AN, která se dotýká paraboly v hlavním vrcholu.

Tvrzení 13.  Problém 8.

 Nechť se těleso pohybuje po obvodu paraboly; najít zákon centrální síly směřující k ohnisku diagramu .

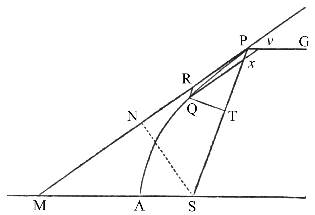Mějme konstrukci stejnou jako v lemmatu 14, a nechť P je těleso na obvodu paraboly; z místa Q do kterého se těleso pohybuje sestrojíme přímku rovnoběžnou s QT  a kolmou k  SP a dále Qv rovnoběžnou s tečnou, která protne průměr PG v bodě v a průvodič SP v bodě x. Nyní, protože trojúhelníky Pxv a  SPM jsou podobné a strany SM a  SP jednoho z nich jsou stejné, jsou strany Px rovné QR a Pv těch ostatních také stejné. Ale podle vlastností kuželoseček [Viz poznámku (39)] je čtverec úsečky Qv rovný obdélníku sestávajícího z latu rekta a úseku Pv, tj. (podle lemmatu 13) je rovný obdélníku 4·PS × Pv nebo 4·PS × QR, a když se body P a  Q přibližují, úsečky Qv a  Qx se (podle důsledku 2 lemmatu 7) mezně rovnají. Proto je v tomto případě Qx² je rovno obdélníku 4·PS × QR. Kromě toho (protože trojúhelníky QxT a  SPN jsou podobné) je Qx² k  QT² jako PS² k  SN², tj. (podle důsledku 1 lemmatu 14) jako PS  k SA, tj. jako 4·PS × QR k  4·SA × QR, a tedy (podle tvrzení 9 knihy 5 Euklidových Základů ) QT² a 4·SA × QR jsou si rovny. Vynásobme tyto rovnosti , potom bude rovno SP² × 4·SA, a proto (podle důsledků 1 a 5 tvrzení 9) je centrální síla nepřímo úměrná SP² ×  4·SA, tj. protože 4·SA je pevné, nepřímo úměrná čtverci vzdálenosti SP. Což se mělo zjistit.

Důsledek 1. Z posledního tvrzení vyplývá, že jestliže se libovolné těleso pohybuje z místa P po přímce PR jakoukoliv rychlostí kamkoliv a ve stejném okamžiku na něj působí centrální síla nepřímo úměrná čtverci jeho vzdálenosti, bude se pohybovat po některé z kuželoseček majících ohnisko ve středu sil a naopak. Jelikož když je dána poloha  tečna, je možno popsat kuželosečku mající určitou křivost v tomto bodě. Ale ta křivost je určena danou centrální silou a rychlostí tělesa; a není možno opisovat dvě různé dráhy, které se navzájem dotýkají a odpovídají stejné centrální síle a stejné rychlosti.

Důsledek 2. Jestliže rychlost kterou těleso opouští své místo P je taková, že úsek dráhy PR jím může být opsán v nějakém minimálním zlomku času, a jestliže centrální síla je schopna způsobit pohyb stejného tělesa za stejný čas, těleso se bude pohybovat po určité kuželosečce, jejíž hlavní latus rektum [viz poznámku ] má hodnotu v mezním případě, když se úseky PR a  QR nekonečně zmenšují. K těmto důsledkům počítám spolu s elipsou i kružnici, ale ne případ, kdy těleso padá rovně k centru.

Tvrzení 14.  Věta 6.

 Když několik těles obíhá okolo jednoho středu a centrální síla je nepřímo úměrná čtverci jejich vzdálenosti od středu, tvrdím, že hlavní laty rekta jejich orbit jsou úměrné čtvercům ploch, které opíší jejich průvodiče vztažené ke středu sil za stejný čas .

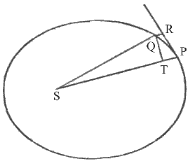Protože (podle důsledku 2 tvrzení 13) je latus rektum roven veličině jako mezní výsledek když se body P a  R přibližují. Ale mizející úsečka QR je v daném čase rovna působící centrální síle to je (podle hypotézy) nepřímo úměrné SP². A tedy je úměrné QT² × SP², tj. latus rektum je úměrný čtverci plochy QT × SP. Což se mělo dokázat.

Důsledek. Jelikož celková plocha elipsy jí úměrný obdélník sestavený z os je úměrný odmocnině z latu rekta a době oběhu. Jelikož celková plocha je úměrná ploše QT×SP, která je opsána za daný čas, vynásobené dobou oběhu.

Tvrzení 15.  Věta 7.

Za stejných předpokladů tvrdím, že čtverce oběžných dob u elips jsou úměrné třetím mocninám hlavních os .

Jelikož vedlejší osy jsou geometrickým průměrem hlavní osy a latu rekta a tedy obdélník sestavený z os je roven odmocnině z latu rekta a 3/2 mocnin hlavní osy. Ale tento obdélník je (podle důsledku tvrzení 14) je úměrný odmocnině z latu rekta a oběžné doby. Vydělme rovnici odmocninou z latu rekta, a výsledkem bude, že čtverce oběžných dob jsou v poměru třetích mocnin hlavních os. Což se mělo dokázat.

Důsledek. A tedy oběžné doby jsou stejné jako u kružnic, jehož poloměry jsou rovné hlavním osám elips.

Tvrzení 16.  Věta 8.

Za stejných předpokladů, když vedeme tělesy přímky tak, aby se dotýkaly jejich drah v místech, kde se nacházejí, a když na tyto komice spustíme ze společného ohniska kolmice, tvrdím, že rychlosti bodů jsou nepřímo úměrné těmto kolmicím a přímo úměrné hlavním latům rektům drah  .

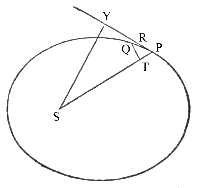Z ohniska S spustíme na tečnu PR kolmici SY, potom rychlost tělesa P bude nepřímo úměrná odmocnině . Jelikož tato rychlost je úměrná mizejícímu oblouku PQ opsanému za daný časový interval (podle lemmatu 7), tedy jako tečna PR, a vzhledem k úměře PR ke QT je jako SP  k SY, bude úměrná též výrazu , čili nepřímo úměrná SY a přímo úměrný SP × QT. A protože výraz SP × QT je úměrný ploše opsané za daný čas, je (podle tvrzení 14) úměrný odmocnině z latu recta. Což se mělo dokázat.

Důsledek 1. Hlavní laty rekta jsou úměrné čtvercům kolmic a čtvercům rychlostí.

Důsledek 2. Rychlosti těles v nejmenší a největší vzdálenosti od společného ohniska jsou nepřímo úměrné vzdálenostem a přímo úměrné odmocnině z hlavních latů rekt. Jelikož kolmice nyní splývají s průvodiči.

Důsledek 3. A tak rychlost na kuželosečkách v největší a nejmenší vzdálenosti od ohniska je k rychlosti, se kterou by se těleso pohybovalo po kružnici se stejnou vzdáleností od středu ve stejném poměru jako odmocnina hlavního latu recta k odmocnině dvojnásobku této vzdálenosti.

Důsledek 4. Rychlosti těles obíhajících po elipsách jsou v jejich středních vzdálenostech od společného ohniska stejné jako rychlosti těles obíhajících v kruzích ve stejných vzdálenostech, a to je (podle důsledku 6 tvrzení 4) v opačném poměru než odmocniny ze vzdáleností. Kolmice nyní souhlasí s malými poloosami, a ty jsou geometrickým průměrem mezi vzdálenostmi a laty rekty. Když složíme převrácenou hodnotu tohoto poměru s odmocninou poměru latu rekta, dostáváme nepřímou úměrnost ke vzdálenosti.

Důsledek 5. Na stejném diagramu, a dokonce na různých diagramech, jejichž laty rekta jsou stejná je rychlost těles nepřímo úměrná dělce kolmic spuštěných z ohniska na tečny.

Důsledek 6. U paraboly je rychlost nepřímo úměrná odmocnině vzdálenosti tělesa od středu diagramu, u elipsy se rychlost mění v poměru, který je větší než tento a u hyperboly v poměru, který je menší. Neboť (podle důsledku 2 lemmatu 14) je kolmice spuštěná z ohniska na tečnu paraboly úměrná odmocnině vzdálenosti. U hyperboly je kolmice menší a u elipsy větší, než odpovídá tomuto poměru.

Důsledek 7. U paraboly je rychlost tělesa v libovolné vzdálenosti od ohniska k rychlosti tělesa obíhajícího v kruhu ve stejné vzdálenosti od středu v poměru odmocniny poměru 2 : 1; u elipsy je menší a u hyperboly větší než tento poměr. Neboť podle důsledku 2 tohoto tvrzení je rychlost ve vrcholu paraboly v tomto poměru, a dále podle důsledku 6 tohoto tvrzení a důsledku 6 tvrzení 4 je tento poměr stejný ve všech vzdálenostech. Proto je též u paraboly rychlost v kterémkoliv místě  rovna rychlosti tělesa obíhajícího v poloviční vzdálenosti; u elipsy je menší a u hyperboly větší.

Důsledek 8. Rychlost tělesa obíhajícího po kuželosečce je k rychlosti tělesa obíhajícího po kružnici ve vzdálenosti poloviny hlavního latu rekta kuželosečky ve stejném poměru, v jakém je tato vzdálenost k délce kolmice spuštěné z ohniska na tečnu kuželosečky. To je zřejmé z důsledku 5.

Důsledek 9. Proto, jelikož (podle důsledku 6 tvrzení 4) je rychlost tělesa obíhajícího po této kružnici k rychlosti tělesa obíhajícímu po jiné kružnici v opačném poměru než odmocniny vzdáleností, vyplývá z rovnosti poměrů, že rychlost tělesa obíhajícího po kuželosečce bude ve stejném poměru k rychlosti tělesa obíhajícího po kružnici ve stejné vzdálenosti, jako je geometrický průměr mezi touto společnou vzdáleností a polovinou hlavního latu rekta kuželosečky a délkou kolmice spuštěnou ze společného ohniska na tečnu kuželosečky.

Tvrzení 17.  Problém 9.

Předpokládejme, že centrální síla je nepřímo úměrná čtverci vzdálenosti těles od centra a že absolutní hodnota této síly je známa; požaduje se nalezení křivky kterou těleso opíše, když vyletí z daného místa danou rychlostí podél dané přímky .

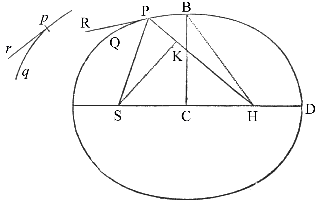Nechť centrální síla mířící k bodu S je taková, že těleso p obíhá jejím působením po nějaké dané dráze pq, a nechť se má určit jeho rychlost v místě p. Nechť těleso P vyletí z místa P podél přímky PR danou rychlostí a nechť je potom odkloněno z této dráhy na kuželosečku PQ  působením centrální síly. Potom přímka PR se bude dotýkat kuželosečky v bodě P. Nechť nějaké přímka pr se též dotýká dráhy pq v bodě p, a když uvážíme kolmici spuštěnou z bodu S na tuto tečnu, hlavní latus rectum  kuželosečky bude (podle důsledku 1 tvrzení 16) k hlavnímu latu rektu dráhy v poměru vypočteném ze čtverců kolmic a čtverců rychlostí a je tedy dán. Označme L latus rektum kuželosečky. Ohnisko S kuželosečky je též dáno. Nechť úhel RPH je doplňkem úhlu RPS do přímého úhlu, potom přímka PH, na které se nachází druhé ohnisko, má známou pozici. Spustíme kolmici SK k  PH a sestrojíme vedlejší poloosu BC. Potom výraz

SP² - 2·KP × PH + PH²

bude [podle tvrzení 13 knihy 2 Euklidových Základů [aplikovaného na trojúhelník PSH]] roven výrazům

SH² = 4·CH² = 4·BH² - 4·BC² = (SP + PH)² - L × (SP + PH) = SP² + 2·SP × PH + PH² - L × (SP + PH) .

Přičteme k oběma stranám výraz

2·(KP × PH) - SP² - PH² + L × (SP + PH)

a dostaneme rovnost

L × (SP + PH) = 2·(SP × PH) + 2·(KP × PH),

čili L× (SP + PH) bude k  PH jako 2·SP + 2·KP k L. A tak je PH dané jak délkou tak polohou. Speciálně, pokud rychlost tělesa v bodě P je taková, že latus rektum L je menší než 2·SP + 2·KP, bude PH ležet na stejné straně tečny PR jako úsečka PS, a tak bude dráha eliptická a bude daná ohnisky S a  H a hlavní osou SP + PH. Ale když je rychlost tělesa tak velká, že latus rektum L je rovno 2·SP + 2·KP, potom  délka PH  bude nekonečná a v souhlase s tím se dráha stane parabolou, jejíž osa SH  bude rovnoběžná s PK. Jestliže těleso letí ze svého místa P s ještě větší rychlostí, potom úsečka PH  bude na druhé straně tečny, a tak, protože tečna prochází mezi ohnisky, dráha se stává hyperbolou s hlavní osou rovnou rozdílu úseček SP a PH, a tedy bude určena. Neboť jestliže těleso v těchto případech obíhá po takto nalezené kuželosečce, bylo dokázáno v tvrzení 11, 12 a 13, že centrální síla bude nepřímo úměrná čtverci vzdálenosti od středu sil S, a tak křivka PQ je správně určena a těleso jí opíše působením dané síly, když vylétá z bodu P danou rychlostí podél přímky PR dané polohou. Což se mělo udělat.

Důsledek 1. Proto pro každou kuželosečku, když je dán hlavní vrchol D, latus rektum L a ohnisko S, druhé ohnisko H je určeno, když vezmeme DH  k  DS ve stejném poměru, jako latus rektum k rozdílu mezi latem rektem a  4·DS. Jelikož poměr SP + PH  k  PH  je jako 2·SP + 2·KP  k  L je v případě tohoto důsledku rovna DS + DH  k DH jako 4·DS  k L.

Důsledek 2. Proto, je-li dána rychlost tělesa v hlavním vrcholu D, dráha bude nalezena rychle, totiž vezmeme-li její latus rektum k dvojnásobku vzdálenosti DS jako čtverec poměru dané rychlosti tělesa obíhajícího v kruhu ve vzdálenosti DS (důsledek 3 tvrzení 16) a potom vzít DH  k  DS jako latus rektum k rozdílu mezi latem rektem a  4·DS.

Důsledek 3. Proto také, když se těleso pohybuje kdekoliv po kuželosečce a je vychýleno ze své dráhy impulsem, potom dráha po které bude pokračovat může být samozřejmě nalezena. Jelikož složením vlastního pohybu tělesa s pohybem, jaký by tento impuls samostatně generoval, bude nalezen pohyb, jakým bude těleso následovat z daného místa působení impulsu podél přímky dané polohou.

Důsledek 4. A jestliže těleso bude neustále vychylováno určitou silou působící zvenku,její dráha může být určena velmi přesně, když zaznamenáme pořadí řady spojitých změn v mezilehlých bodech.

Komentář

Jestliže těleso P  působením centrálních sil směřujících do daného bodu R pohybuje kdekoliv po obvodu kuželosečky se středem C a má se najít zákon centrální síly, potom sestrojíme CG  rovnoběžnou s poloměrem RP  a protínající tečnu PG dráhy v bodě G, potom síla (podle důsledku 1 a komentáři k tvrzení 10 a důsledku 3 tvrzení 7) bude jako .

(Následují pouze vybrané části prvé knihy)

Sekce 11.

O přitažlivých silách sférických těles .

Až k tomuto místu jsem vykládal o pohybech těles přitahovaných k nehybnému středu, což ovšem není běžné v přirozeném světě. Jelikož přitažlivost je vždy směřována k tělesům, a podle třetího zákona jsou působení přitahujícího a přitahovaného tělesa vždy vzájemná a stejně velká; a tak když máme dvě tělesa, ani přitahující ani přitahované těleso nemůže být v klidu, ale obě (podle důsledku 4 zákonů) obíhají kolem společného těžiště pokud se přitahují navzájem; a pokud máme více než dvě tělesa, která jsou buď všechna přitahována a přitahují jedno těleso nebo se přitahují navzájem, tato tělesa  se musí navzájem pohybovat tak, aby bylo společné těžiště buď v klidu nebo se pohybovalo rovnoměrně přímočaře dopředu. Proto se teď chystám vykládat o pohybu těles, která se navzájem přitahují, a budu centrální síly nazývat přitažlivostí, ačkoliv, když hovoříme jazykem fyziky, měly by být nazývány spíše impulsy. Ale protože máme co dělat s matematikou, ponecháváme stranou debatu o fyzice a používáme podobný jazyk, aby nám snáze rozuměli matematicky orientovaní čtenáři.

Tvrzení 57.  Věta 20.

Dvě tělesa, která se navzájem přitahují, opisují podobné obrazce kolem svého společného těžiště a také kolem sebe navzájem . 

Neboť vzdálenosti těchto těles od jejich společného těžiště jsou nepřímo úměrné jejich hmotám a proto jsou v tomto poměru složena na spojnici obou těles s těžištěm. Tyto spojnice navíc rotují spolu s tělesy stejným úhlovým pohybem, protože těžiště i tělesa leží vždy na přímce a nemění svůj náklon vůči sobě. A spojnice jsou vůči sobě neustále v daném vzájemném poměru a rotují spolu s planetami na koncích a stejným úhlovým pohybem opisují podobné pohyby, zatímco těžiště je v klidu nebo rovnoměrném přímočarém pohybu, který není úhlový. Proto jsou dráhy opisované těmito tělesy podobné. Což se mělo dokázat.

Tvrzení 58.  Věta 21.

Jestliže se dvě tělesa navzájem přitahují libovolnými silami a současně obíhají kolem společného těžiště, tvrdím, že by obíhala kolem některého z těles, kdyby bylo nehybné, po dráhách podobných a stejných, jaké tělesa opisují kolem sebe působením stejné síly . 

Nechť tělesa S a  P obíhají kolem jejich společného těžiště C a pohybují se z bodů S do T a  P do Q. Z daného bodu s nechť sp a  sq jsou pořád stejné a rovnoběžné s  SP a TQ; potom křivka pqv, kterou bod p opisuje při oběhu okolo nehybného bodu s, je podobná a stejná jako křivky, které tělesa S a  P opisují navzájem kolem sebe, a (podle tvrzení 57) tato křivka pqv bude podobná křivce PQV, kterou ta samá tělesa opisují kolem společného těžiště C; a to vzhledem k dané úměrnosti úseček SC, CP a  SP nebo sp navzájem.

Případ 1. Společné těžiště C (podle důsledku 4 zákonů) je buď v klidu nebo se pohybuje rovnoměrně přímočaře vpřed. Předpokládejme nejdříve, že je v klidu a do bodů s a p jsou umístěna dvě tělesa, jedno nepohyblivé do bodu s a jedno pohyblivé do bodu p., podobná nebo stejná jako tělesa S a P. Dále nechť se přímky PR a pr dotýkají křivek PQ a pq v bodech P a p, a nechť CQ a cq jsou prodlouženy do bodů R a r. Potom, jelikož obrazce CPRQ a sprq jsou podobné, bude RQ k rq v témž poměru jako CP k sp a tak je dán poměr. V souhlase s tím, pokud síla, kterou těleso P je přitahováno k tělesu S, a tedy k okamžitému středu C, je ve stejném daném poměru k síle, kterou je těleso p přitahováno ke středu s, a tak za stejnou dobu budou tyto síly stále přitahovat tělesa z tečen PR a pr na oblouky PQ a pq  na vzdálenosti RQ a rq, které jsou jim úměrné; a proto ta poslední síla bude nutit těleso p obíhat po dráze na křivce pqv, která bude podobná křivce PQV, po které ta prvá síla nutí těleso P obíhat po jeho dráze, a obíhání bude dokončeno za stejnou dobu. Ale ty síly nejsou navzájem ve poměru CP k sp, ale jsou si navzájem rovné (protože tělesa S a s, P a p jsou podobná a stejná, a vzdálenosti SP a sp jsou stejné); proto tělesa budou za stejný čas stejně vychýlena od tečen; a tedy, jelikož druhé těleso  musí být vychýleno na větší vzdálenost rq, je zapotřebí delší doba, která je úměrná odmocnině ze vzdáleností, jelikož (podle lemmatu 10) jsou dráhy opsané na samém počátku pohybu úměrné odmocnině z časů. Proto rychlost tělesa p musí být k rychlosti tělesa P v poměru odmocniny poměru vzdálenosti sp ke vzdálenosti CP, a tak oblouky pq a PQ, které jsou v prostém poměru , jsou opsány za doby, které jsou odmocninami ze vzdáleností. Potom tělesa P a p, která jsou vždy přitahována stejnými silami, budou  opisovat kolem středů C a s podobné obrazce PQV a pqv, ze kterých pqv je podobný a stejný jako obrazec, který těleso P opisuje kolem pohyblivého tělesa S. Což se mělo dokázat.

Případ 2. Předpokládejme nyní, že společné těžiště, spolu s prostorem ve kterém se tělesa navzájem pohybují, se pohybuje rovnoměrně přímočaře vpřed; potom (podle důsledku 6 zákonů) se všechny pohyby v tomto prostoru budou odehrávat jako v případě 1. A tedy tělesa budou navzájem opisovat obrazce, které jsou stejné jako předtím a které budou podobné a stejné jako obrazec pqv.

Důsledek 1. Proto (podle tvrzení 10) dvě tělesa, která se navzájem přitahují silou úměrnou jejich vzdálenosti, budou opisovat soustředné elipsy kolem společného těžiště a též kolem sebe navzájem; a naopak, když opisují takové křivky, jsou síly úměrné vzdálenosti.

Důsledek 2. A (podle tvrzení 11, 12 a 13) dvě tělesa budou působením sil nepřímo úměrných čtverci jejich vzdálenosti opisovat kolem společného těžiště a též kolem sebe navzájem, kuželosečky s ohniskem v tomto těžišti, kolem kterého jsou obrazce opisovány. A naopak, pokud opisují takové obrazce, centrální síla je nepřímo úměrná jejich vzdálenosti.

Důsledek 3. Jakákoliv dvě tělesa obíhající po dráze okolo společného těžiště opisují průvodiči vycházejícími z tohoto těžiště a také jejich spojnicí plochy úměrné času.

Tvrzení 59.  Věta 22.

Oběžné doby dvou těles  S a  P obíhajících okolo společného těžiště  C jsou k oběžným dobám jednoho z těles obíhajícího druhého nehybného tělesa S a opisující podobné a stejné obrazce, která tělesa opisují okolo sebe, jako odmocnina poměru hmotnosti druhého tělesa  S k součtu hmotností  těles  S + P .

Neboť, podle důkazu tvrzení 58, časy ve kterých libovolné podobné oblouky PQ a pq jsou opsány jsou v poměru odmocniny vzdáleností CP a SP nebo sp, to jest, jako odmocnina poměru hmotnosti tělesa S k součtu hmotností těles S + P. A jejich složením zjistíme, že součet časů, za který jsou opsány podobné oblouky PQ a pq , tj. celkové časy, za které jsou opsány celé podobné obrazce, jsou ve stejném poměru. Což se mělo dokázat.

Tvrzení 60.  Věta 23.

Jestliže dvě tělesa S a  P, která se přitahují silou nepřímo úměrnou čtverci jejich vzdálenosti obíhají kolem společného těžiště, tvrdím, že hlavní osa elipsy které jedno z těles P opisuje při svém pohybu okolo druhého tělesa S bude k hlavní ose elipsy, kterou by to samé těleso P mohlo opisovat za stejnou oběžnou dobu okolo druhého tělesa S v klidu je v témž poměru jako součet hmotností obou těles S + P a třetí odmocninou součinu čtverce tohoto součtu a hmotnosti druhého tělesa S .

 Neboť pokud jsou takto opisované elipsy navzájem rovné, potom oběžné doby budou (podle tvrzení 59) v poměru odmocniny poměru hmotnosti tělesa S a součtu hmotností obou těles S + P. Nechť je oběžná doba druhé elipsy zmenšena ve stejném poměru, potom budou oběžné doby stejné; ale hlavní osa  druhé elipsy bude  (podle tvrzení 15) zmenšena v 3/2 poměru předchozího poměru, to jest v poměru, jehož třetí mocninou je poměr S k S + P; a proto hlavní osa druhé elipsy bude k hlavní ose prvé elipsy jako třetí odmocnina součinu čtverce S + P a S k S + P. Což se mělo dokázat.

Tvrzení 61.  Věta 24.

Jestliže dvě tělesa S a  P, která se přitahují jakoukoliv silou a nepůsobí ani netlačí na ně nic jiného, jejich pohyb bude stejný, jako kdyby se navzájem nepřitahovala, ale přitahovaly je stejné síly třetího tělesa umístěného v jejich těžišti. A zákon přitažlivých sil bude stejný pokud jde o vzdálenost těles od společného těžiště a s ohledem na celkovou vzdálenost těles .

Neboť síly, kterými se tělesa navzájem přitahují, směřují k tělesům, směřují ke společnému těžišti mezi nimi a proto jsou stejné jako kdyby vycházely s tělesa mezi nimi. Což se mělo dokázat.

A jelikož je daný pevný poměr vzdáleností každého ze dvou těles od společného těžiště ke vzdálenosti mezi tělesy, existuje také pevný poměr libovolné mocniny takové vzdálenosti ke stejné mocnině druhé vzdálenosti; stejně jako poměr libovolné veličiny odvozené libovolným způsobem z takové vzdálenosti a jistého počtu daných veličin k druhé veličině odvozené stejným způsobem z druhé vzdálenosti a stejného počtu daných veličin, které mají příslušný poměr ke druhé vzdálenosti. Vzhledem k tomu, pokud síla kterou jedno těleso je přitahováno k jinému je přímo nebo nepřímo úměrné vzájemné vzdálenosti obou těles nebo libovolné mocnině této vzdálenosti nebo nakonec jako libovolná veličina odvozená jakýmkoliv způsobem z této vzdálenosti a daných veličin, potom stejná síla kterou je těleso přitahováno ke společnému těžišti bude v jakémkoliv přímém či nepřímém poměru ke vzdálenosti nebo nakonec  jako veličina odvozená stejným způsobem ze vzdálenosti a analogických daných veličin. Tj. zákon přitažlivé síly bude stejný vzhledem k jakékoliv ze vzdáleností. Což se mělo dokázat.

Tvrzení 65.  Věta 25.

Více těles, jejichž přitažlivé síly klesají se čtvercem vzájemné vzdálenosti od jejich středů se mohou navzájem pohybovat po elipsách a průvodiči k jejím ohniskům opisovat plochy úměrné přibližně času .

 V tvrzení 64 byl ukázán příklad ve kterém obíhá více těles přesně po elipsách. Čím více se zákon síly odchyluje od zákona, který tam platil, tím více tělesa porušují svůj vzájemný pohyb; nemůže se stát ani to, že by se tělesa pohybovala přesně po elipsách jako v popsaném případě, pouze udržují pevné poměry vzájemných vzdáleností. Ovšem v následujících případech nebudou dráhy příliš odlišné od elips.

Případ 1. Předpokládejme, že několik lehčích těles obíhá okolo jednoho mnohem většího v různých vzdálenostech, a že že absolutní síly úměrné jejich hmotnostem míří ke každému z nich. Potom, jelikož společné těžiště všech těles (podle důsledku 4 zákonů) je buď v klidu nebo nebo se pohybuje rovnoměrně přímočaře vpřed, a představte si, že ta menší tělesa jsou tak malá, že to velké těleso se nikdy citelně nevzdálí od tohoto těžiště. V tomto případě bude větší těleso bez citelné chyby v klidu nebo se bude pohybovat rovnoměrně přímočaře vpřed, zatímco ta lehčí budou obíhat okolo toho většího po elipsách a jejich průvodiče, které je s ním spojují, budou opisovat plochy úměrné času, až nato, že s určitými chybami způsobené buď odchylkou většího tělesa od tohoto společného těžiště nebo vzájemným působením menších těles na sebe. Ta menší tělesa ovšem mohou být zmenšována  odchylka a vzájemné působení není menší než zadaná hodnota, a tedy dokud jejich dráhy nebudou shodné s elipsami a plochy neodpovídají času bez jakékoliv chyby, která není menší než libovolná zadaná hodnota. Což se mělo dokázat.

Případ 2. Nyní si představme systém menších těles obíhajících  právě popsaným způsobem kolem mnohem těžšího tělesa, nebo jakýkoliv jiný systém dvou těles obíhajících okolo sebe, která se pohybují rovnoměrně přímočaře vpřed a současně jsou vychylována stranou silou jiného ještě většího tělesa, které je ve velké vzdálenosti. Potom, jelikož stejné zrychlující síly kterými jsou tělesa vychylována podél rovnoběžek nemění vzájemnou situaci těles, ale způsobí, že celý systém bude současně přemísťován, zatímco vzájemné pohyby částí systému jsou zachovány; je zjevné, že nenastane vůbec žádná změna pohybu těles přitahovaných k sobě působená větším tělesem, dokud taková změna nebude způsobena nerovností urychlující přitažlivosti nebo ze vzájemné odchylky přímek, podle kterých přitahování působí. Předpokládejme tedy, že všechny urychlující přitažlivosti k těžšímu tělesu vzhledem jiným je nepřímo úměrné čtvercům vzdáleností; potom zvětšováním vzdálenosti těžšího tělesa, dokud rozdíly (vzhledem k délce) mezi průvodiči spojujícími toto těleso s jinými tělesy a jejich vzájemné odchylky jsou menší než libovolná zadaná hodnota, potom vzájemný pohyb částí systému se zachová bez chyb, které by byly větší než libovolná předem zadaná hodnota. A vzhledem k malým vzájemným vzdálenostem těchto částí systému je celý systém přitahován jako by to bylo jedno těleso; a tedy svým těžištěm bude opisovat kolem těžšího tělesa některou kuželosečku (konkrétně hyperbolu nebo parabolu, pokud je přitažlivost malá, a elipsu, pokud je přitažlivost větší) a průvodičem k těžšímu tělesu bude opisovat plochy úměrné času bez chyb kromě těch, které mohou být působeny vzdálenostmi mezi částmi, a ty jsou přípustně malé a mohou být zmenšeny podle potřeby. Což se mělo dokázat.

Na základě podobných argumentů je možno pokračovat se složitějšími příklady donekonečna.

Důsledek 1. V případě 2, čím blíže se těžší těleso přibližuje k systému dvou nebo více těles, tím více bude porušen vzájemný pohyb částí systému působením vzájemných odchylek průvodičů spuštěných z těchto těles na větší těleso.

Důsledek 2. Ale tyto poruchy budou větší, pokud urychlující síly částí systému vzhledem k většímu tělesu nebudou navzájem v obráceném poměru jako čtverce vzdáleností od velkého tělesa, zejména pokud nerovnost tohoto působení je větší než nerovnost úměry vzdáleností od většího tělesa. Neboť pokud urychlující síla, působící stejně a podél rovnoběžek, žádným způsobem nenarušuje vzájemný pohyb částí systému, bude nutně působit vznik poruch při nerovnosti tohoto působení., a tyto poruchy budou větší nebo menší podle toho, zda tyto nerovnosti jsou menší nebo větší. Nadbytek silného působení na některé těleso, které nepůsobí na ostatní, bude nutně měnit vzájemnou situaci těles. A tato porucha, přičtena k poruše vznikající působením odchylek nebo nerovnosti spojnic, způsobí celkově větší poruchu.

Důsledek 3. Proto, pokud části systému se bez znatelných poruch pohybují po elipsách nebo po kruzích, je zřejmé, že tyto části buď nejsou vychylovány vůbec (samozřejmě až na malé výjimky) urychlujícími silami směřujícími k jinému tělesu, nebo jsou vychylovány stejně a velmi přesně podél rovnoběžek.

Tvrzení 66.  Věta 26.

Tři tělesa, jejichž síly klesají se čtvercem vzdálenosti, se přitahují navzájem, a vzájemná urychlující přitažlivost jakékoliv dvojice vůči třetímu tělesu je nepřímo úměrná čtvercům vzdáleností, a menší tělesa obíhají okolo většího. Potom tvrdím, že vnitřní těleso obíhá kolem nejvnitřnějšího a největšího tělesa a opisuje průvodiči spuštěnými k němu plochy přibližně úměrné času a obrazce přibližně ve tvaru elips, které mají svá ohniska přibližně v průsečíku průvodičů a které by působilo největší těleso svou přitažlivostí , kdyby to větší v klidu nebylo přitahováno menším nebo bylo mnohem více či mnohem méně přitahováno nebo buď mnohem méně nebo mnohem více působilo  .

 Je to zcela jasné z demonstrace druhého důsledku, ale bude to dokázáno přehlednějšími a přesvědčivějšími argumenty.

Případ 1. Nechť lehčí tělesa P a  S obíhají ve stejné rovině okolo největšího tělesa T, nechť tělwso P  opisuje vnitřní dráhu PAB a těleso S vnější dráhu ESE. Nechť SK je střední vzdálenost mezi tělesy P a S, a nechť urychlující přitažlivost  tělesa P vůči S v této střední vzdálenosti je představována stejnou úsečkou SK. Nechť SL je k  SK jako SK² k SP², potom SL bude urychlující přitažlivost tělesa P vůči S v libovolné vzdálenosti SP. Spojíme PT a rovnoběžně s ní sestrojíme LM  protínající ST v bodě M; potom přitažlivost SL se rozloží (podle důsledku 2 zákonů) na přitažlivosti SM a LM. A tak těleso P  bude vychylováno třemi zrychlujícími silami. Jedna taková síůa míří k T a vzniká se vzájemné přitažlivosti těles T a P. Působením této síly (ať u ž je těleso T v klidu nebo se vlivem této síly pohybuje) musí těleso P poloměrem PT opisovat kolem tělesa T plochy úměrné času a musí též opisovat elipsu, jejíž ohnisko je ve středu tělesa T. To je jasné z tvrzení 11 a důsledků 2 a 3 tvrzení 58.

Druhou silou je složka přitažlivosti LM, která (protože míří od P  k T ) bude po přidání k prvé síle působit tak, že opsaná plocha bude nadále úměrná času podle důsledku 3 tvrzení 58. Ale protože není nepřímo úměrná čtverci vzdálenosti PT, bude se spolu s prvou silou skládat na sílu, která se liší od této úměry, a to tím více, čím je tato síla silnější v poměru k prvé síle, vše ostatní je stejné. Neboť (podle tvrzení 11 a důsledku 2 tvrzení 58) musí síla působící pohyb po elipse kolem ohniska T mířit k tomuto ohnisku a být nepřímo úměrná čtverci vzdálenosti PT, zatímco tato složená síla tím, že nesplňuje tuto úměru způsobí, že dráha PAB se odchýlí od tvaru elipsy s ohniskem v T, a to tím více, čím větší je odchylka od této úměrnosti; a odchylka od této úměry bude tím větší, čím větší bude poměr druhé síly LM  k té prvé větší síle, vše ostatní zůstane stejné.

Ale třetí síla SM přitahující těleso P podél přímky rovnoběžné s  ST se bude spolu s předchozími silami skládat na sílu, která již nesměřuje od P  k  T a  odklání se od tohoto směru tím více, čím větší bude tato třetí síla v poměru k předchozím silám, když bude vše ostatní stejné; a tato složená síla bude tedy působit odchylku od této úměrnosti tím větší, čím větší bude tato síla v poměru k ostatním silám. Tato třetí síla zvětší odchylku dráhy PAB od zmíněného eliptického tvaru ze dvou důvodů: nejenže ta síla nemíří od P  k T, ale navíc není nepřímo úměrná čtverci vzdálenosti PT. Jakmile těmto věcem porozumíme, je zřejmé, že plochy budou tím více úměrné času čím bude tato třetí síla menší, když ostatní síly zůstanou stejné jako dříve, a že dráha PAB se bude blížit zmíněnému elipsoidu tím více, když jak ta druhá tak ta třetí síla (ale zejména ta třetí) bude co nejmenší, když prvá síla zůstane stejná.

Nechť urychlující přitažlivost tělesa T vůči S je představována úsečkou SN, potom pokud by urychlující přitažlivosti SM a  SN byly stejné a rovnoběžné, nenastala by vůbec žádná změna ve vzájemné situaci těchto dvou těles. V tomto případě by jejich vzájemný pohyb byl (podle důsledku 6 zákonů) stejný jako kdyby žádné přitažlivosti nebylo. A z těch samých důvodů, kdyby přitažlivost SN  byla menší než přitažlivost SM, zrušila by část SN přitažlivosti SM a jen část MN, která by zbyla, a jejím působením by byly narušeny úměrnost časů a ploch a eliptický tvar dráhy. A podobně, kdyby působení přitažlivosti SN  bylo větší než přitažlivost SM, porucha úměrnosti a dráhy by vznikla jen působením samotného rozdílu MN. A tak SM, třetí výše zmíněná přitažlivost, je vždy zmenšena přitažlivostí SN na přitažlivost MN, zatímco prvá a druhá přitažlivost zůstanou zcela beze změny, a tedy plochy a čas jsou blíže k úměrnosti, a dráha PAB se nejvíce přiblíží výše zmíněnému eliptickému tvaru, když přitažlivost MN je buď nulová nebo co nejmenší, tj. když urychlující přitažlivost těles P a  T  k tělesu S  se budou co nejvíce rovnat, jinými slovy, když přitažlivost SN není ani nulová ani menší než nejmenší ze všech přitažlivostí SM, ale někde kolem střední hodnoty mezi maximem a minimem těchto přitažlivostí SM, to jest, ani o moc větší ani o moc menší než přitažlivost SK. Což se mělo dokázat.

Případ 2. Nyní nechť  menší tělesa P a S obíhají kolem největšího tělesa T v různých rovinách; potom síla LM, působící podél úsečky PT  ležící v rovině dráhy PAB, bude mít stejný účinek jako předtím a nebude vychylovat těleso P z roviny jeho dráhy. Ale druhá síla NM, působící po úsečce rovnoběžné s ST (a tedy, když je těleso S mimo spojnici uzlových bodů, je vychýlena z roviny PAB), kromě poruchy v podélném směru, který byl již vyložen, způsobí poruchu pohybu v příčném směru a bude přitahovat těleso P mimo rovinu jeho dráhy. A tato porucha v jakékoliv vzájemné poloze těles P a T, bude jako působící síla MN, a tedy se stane nejmenší když je MN  nejmenší, tj. (jak jsem již vyložil), když přitažlivá síla SN není o mnoho větší ani o mnoho menší než přitažlivost SK. Což se mělo dokázat.

Důsledek 1. Proto je snadné zjistit, že pokud několik menších těles P, S, R, … obíhá kolem největšího tělesa T, potom pohyb nejvnitřnějšího tělesa P bude nejméně porušen přitažlivostí vnějších těles když je největší těleso přitahováno a působí na něj vnější tělesa (podle poměru přitažlivých sil) stejným způsobem jako ostatní tělesa na sebe navzájem.

Důsledek 2. V systému tří těles T, P a S, je-li vzájemná urychlující přitažlivost jakékoliv dvojice vůči třetímu tělesu je nepřímo úměrná čtvercům vzdáleností, těleso P  bude opisovat svým průvodičem PT okolo bodu T plochu rychleji blízko jejich konjunkce A a opozice B než v kvadraturách C a D. Neboť libovolná síla, která vychyluje těleso P a nevychyluje T a která nepůsobí podél přímky PT, urychluje nebo zpomaluje opisování ploch podle toho, zda jej její směr v souhlase nebo v protikladu . Taková je síla NM. Při průchodu tělesa P od C do A působí tato síla souhlasně a urychluje pohyb, dále až po bod D působí protikladně a zpomaluje pohyb, potom souhlasně do bodu B a nakonec protikladně při průchodu od B do C.

Důsledek 3. A podle stejných argumentů je zřejmé, že těleso P, za jinak stejných podmínek se pohybuje rychleji při konjunkci a opozici než v kvadraturách.

Důsledek 4. Dráha tělesa P za jinak stejných podmínek je zakřivenější v kvadraturách než při konjunkci a opozici. Neboť rychlejší tělesa jsou méně vychylována z přímé dráhy. A kromě toho v konjunkci a opozici působí síla KL nebo NM  proti síle, která těleso vychyluje od přímočarého pohybu a proto tu sílu zmenšuje a těleso P  bude méně vychylováno z přímé dráhy když je méně vychylováno k tělesu T.

Důsledek 5. V souhlase s tím, těleso P za jinak stejných podmínek se bude vzdalovat od tělesa T dále v kvadraturách než v konjunkci a opozici. Platí to, pokud neuvažujeme změnu výstřednosti. Neboť jestliže dráha tělesa P  je výstředná, její výstřednost (jak bude krátce ukázáno v důsledku 9 tohoto tvrzení) se stane větším když jsou apsidy v syzygách, a tak se může stát, že těleso P, které dosáhlo apo apsidu, může být vzdálenější od tělesa T v syzygách než v kvadraturách.

Důsledek 6. Jelikož centrální síla ústředního tělesa T, které udržuje těleso P na jeho dráze, je zesilována  v kvadraturách přidáním síly LM a je zmenšována v syzygách odečtením síly KL, a vzhledem k velikosti síly KL [která je větší než LM] je více zvětšena než zmenšena.a jelikož centrální síla (podle důsledku 2 tvrzení 4) je v přímém poměru ke vzdálenosti TP a nepřímém poměru čtverce oběžné doby, je zřejmé, že tato složená síla je zmenšována působením síly KL, a proto oběžná doba (za předpokladu nezměněné vzdálenosti TP) je zmenšena v poměru odmocniny poměru, ve kterém je centrální síla zmenšena. Je proto dále zřejmé, že, pokud uvážíme zmenšení nebo zvětšení poloměru, oběžná doba vzroste více nebo je zmenšena méně než 3/2 mocnina tohoto poloměru podle důsledku 6 tvrzení 4. Když síla centrálního tělesa postupně slábne, těleso P, přitahováno méně a méně, bude neustále dále a dále od středu T; naopak, když se síla zmenšuje, bude stále blíže a blíže. A tedy když působení vzdáleného tělesa S, kterým je síla zmenšena, se střídavě zesiluje a zeslabuje, bude vzdálenost TP ve stejném poměru střídavě zvětšována a zmenšována, a oběžná doba se bude růst a klesat v poměru vypočteném z 3/2 mocniny poměru vzdálenosti a odmocniny poměru, ve kterém je centrální síla ústředního tělesa T zvětšována nebo zmenšována zvětšováním nebo zmenšováním působení vzdáleného tělesa S.

Důsledek 7. Z právě uvedeného vyplývá též, že pokud jde o úhlový pohyb os elipsy opisované tělesem P, neboli pohyb čáry apsid, je střídavě zrychlován nebo zpomalován, nicméně zrychlován je více než zpomalován a probíhá souhlasně převahou pohybu vpřed. Neboť síla kterou je těleso P vychylováno k tělesu P v kvadraturách, když síla MN vymizí, se skládá ze síly LM a centrální síly, kterou těleso T přitahuje těleso P. Když se vzdálenost PT zvětší, prvá síla LM se zvětší ve zhruba stejném poměru jako vzdálenost, a druhá síla se zmenší jako čtverec této vzdálenosti, a tak součet těchto sil se zmenší se čtvercem této vzdálenosti, a tak součet těchto sil se zmenší v menším poměru než čtverec vzdálenosti PT, a tedy (podle důsledku 1 tvrzení 45) působí, že apoapsida se vrací. Ale v konjunkci a opozici je síla, kterou je těleso P vychylováno k tělesu T, rozdílem mezi silou, kterou těleso T přitahuje těleso P, a síly KL, a tento rozdíl klesá vzhledem k tomu, že síla KL roste velmi pomalu v poměru ke vzdálenosti PT, v poměru ke vzdálenosti PT větším než je čtverec vzdálenosti PT, a tak (podle důsledku 1 tvrzení 45) působí, že apoapsida se předbíhá. Mezi syzygami a kvadraturami pohyb apoapsidy závisí na obou těchto vlivech dohromady, a tak podle převahy jedné nebo druhé se předbíhá nebo zpožďuje. Vzhledem k tomu, že síla KL je v syzygách zhruba dvakrát větší než síla LM v kvadraturách, rozdíl bude ve stejném smyslu jako síla KL a bude posouvat apoapsidu dopředu. Pravdivost tohoto a předchozího důsledku lze snadno ověřit představou, že systém dvou těles T a P je obklopen ze všech stran více tělesy S, S, S, … která jsou na dráze ESE. Neboť působením těchto těles bude působení T zmenšeno ze všech stran a klesne v poměru větším, než je čtverec vzdáleností.

Důsledek 8. Jelikož ovšem pohyb apsid dopředu nebo dozadu závisí na zmenšování centrální síly, zmenšování nastávající v poměru vzdáleností TP je vždy větší nebo menší než čtverec vzdálenosti TP při průchodu tělesa z dolní do apoapsidy, a také závisí na podobném zvětšení při návratu do periapsidy, a proto je větší když úměra síly v apoapsidě k síle v periapsidě se značně liší od obráceného poměru čtverce vzdáleností, je jasné, že KL nebo NM - LM, síla která se odčítá, bude způsobovat, že apsidy se budou předbíhat v syzygách rychleji a že LM, přidaná síla, způsobí jejich zpomalování v kvadraturách pomaleji. A vzhledem k délce doby, po kterou zrychlené pohybu vpřed nebo zpomalení pohybu vzad pokračuje, tato nerovnost bude ještě větší.

Důsledek 9. Jestliže má těleso působením síly nepřímo úměrné čtverci jeho vzdálenosti od středu obíhat kolem tohoto středu po elipse, a jestliže je potom při svém sestupu z apoapsidy k periapsidě, tato síla by vzhledem k neustálému přičítání nové síly byla zvýšena v poměru, který je větší než zmenšený poměr, a tak je zřejmé, že toto těleso, které je stále přitahováno ke středu neustálým přičítáním této nové síly, bude se odklánět k tomuto středu více, než kdyby bylo přitahováno jen silou rostoucí se čtvercem zmenšující se vzdálenosti, a proto bude opisovat dráhu uvnitř  eliptické dráhy a její periapsida bude dosažena blíže středu než dříve. Proto po přidání nové síly bude výstřednost dráhy zvětšena. A nyní, během výstupu tělesa od periapsidy k apoapsidě bude síla zmenšena ve stejném poměru  těleso se vrátí do své původní vzdálenosti, a tak, když je síla zmenšena ve větším poměru, potom těleso, nyní méně přitahované, vystoupí do větší výšky, a tak výstřednost se ještě zvýší. A tak, když poměr zvětšování a zmenšování centrální síly se zvětšuje při každém oběhu, výstřednost bude neustále růst, a naopak výstřednost bude klesat když poměr klesá.

Nyní v systému těles T, P a S, když apsidy dráhy jsou v kvadraturách, tento poměr zvětšování a zmenšování je nejmenší a stane se největší, když apsidy jsou v syzygách. Když jsou apsidy v kvadraturách, poměr blízko apsid je menší a blízko syzyg je větší než je čtverec vzdáleností, a z většího poměru vzniká dopředný nebo přímý pohyb apoapsid, jak již bylo řečeno. Ale když uvážíme poměr celkového zvětšování nebo zmenšování dopředného pohybu apsid, je tento poměr menší než čtverec poměru vzdáleností Síla v periapsidě je k síle v apoapsidě v poměru, který je menší než čtverec poměru vzdáleností apoapsidy a periapsidy od ohniska elipsy, a naopak v syzygách je síla v periapsidě k síle v apoapsidě v poměru větším než čtverec poměru vzdáleností.

Neboť síly LM v kvadraturách přidávané k silám tělesa T vytvářejí síly v menším poměru, a síly KL v syzygách, odečtené od sil tělesa T, vytvářejí síly ve větším poměru. Proto poměr celkového sestupu a výstupu během průchodu mezi apsidami je menší v kvadraturách a největší v syzygách, a proto běhe průchodu apsid z kvadratur do syzyg je tento poměr neustále zvětšován a zvyšuje výstřednost elipsy, a při průchodu ze syzyg do kvadratur se neustále zmenšuje a zmenšuje výstřednost.

Důsledek 10. K vysvětlení poruch v příčném směru si představme, že rovina dráhy ESE zůstane nepohyblivá, potom z případů právě vyložených poruch je zřejmé, že z dvojice sil NM a ML (což jsou veškeré příčiny poruch) síla ML, která vždy působí v rovině dráhy PAB, nikdy neporuší pohyb v příčném směru. Je rovněž zřejmé, že když jsou vrcholy v syzygách, síla NM, která také působí v téže rovině dráhy, nikdy nenaruší tyto pohyby, ale když jsou vrcholy v kvadratuře, tato síla poruší tyto pohyby v největším rozsahu a bude neustále přitahovat těleso P pryč z roviny jeho dráhy tak, že zmenší odchylku dráhy během přechodu tělesa z kvadratur do syzyg a naopak zvýší tuto odchylku během průchodu ze syzyg do kvadratur. Proto když je těleso v syzygách, odchylka klesne na úplně nejmenší a vrátí se zhruba na stejnou velikost, když těleso dojde k příštímu uzlu.. Ale pokud jsou uzly umístěny v oktantech po kvadraturách, tj. mezi C a A nebo D a B, je možno pochopit z dosud vyloženého, že při průchodu tělesa B z libovolného uzlu do pozice o 90º dále, odchylka roviny se neustále zmenšuje, potom při průchodu o dalších 45º do další kvadratury se odchylka zvětšuje, a dále při příštím průchodu přes dalších 45º k příštímu uzlu se zmenšuje. Proto odchylka se zmenšuje více než zvětšuje a proto je stále menší v každém dalším uzlu než v tom bezprostředně předchozím. A z podobných úvah vyplývá, že odchylka se zvětšuje více než se zmenšuje, když uzlu jsou v ostatních oktantech mezi A a B nebo B a C. A tedy když jsou uzly v syzygách, odchylka je vůbec největší. Při průchodu uzlů ze syzyg do kvadratur se odchylka zmenšuje při každém průchodu tělesa uzly a stává se nejmenší když jsou oba uzly v kvadraturách a těleso je v syzygách, potom poroste se stejným stupněm se kterým se předtím zmenšovala a při průchodu uzlů k nejbližším syzygám se vrátí na původní hodnotu.

Důsledek 11. Když jsou uzly v kvadraturách,  je těleso P neustále vychylováno z roviny své dráhy k S během přechodu z bodu C přes konjunkci A do bodu D a v opačném směru při průchodu z uzlu D přes opozici B do bodu C, z toho je zřejmé, že těleso při svém pohybu z bodu C neustále ustupuje z první roviny CD své dráhy dokud nedosáhne příští uzel, a proto v tomto uzlu, kdy je v největší vzdálenosti od první roviny CD, neprochází rovinou dráhy EST v dalším uzlu D  této roviny, ale v bodě bližším k tělesu S, který se tak stává novým místem uzlu za svým původním místem. Podle stejných argumentů budou uzly ustupovat při průchodu tělesa z tohoto uzlu do uzlu příštího. Proto uzly, když jsou umístěny v kvadraturách, neustále ustupují; v syzygách, když příčný pohyb není porušován, jsou uzly v klidu; v mezilehlých místech, která sdílejí obě podmínky, ustupují méně pomalu; a proto, když uzly buď ustupují nebo jsou v klidu, posouvají se v protisměru při každém oběhu.

Důsledek 12. Všechny poruchy popsané v těchto důsledcích jsou o něco větší při konjunkci těles P a S než při jejich opozici, a to nastává proto, že síly NM a ML jsou větší.

Důsledek 13. A jelikož úměry v těchto důsledcích nezávisí na velikosti tělesa S, všechny předchozí případy, když velikost tělesa S  je pokládána za dostatečně velkou, že systém dvou těles T a P bude obíhat okolo něho. A s růstem velikosti a následně vzrůstu centrální síly (které působí poruchy oběhu tělesa P) se všechny tyto chyby stávají ve stejných vzdálenostech větší než v opačném případě, kdy těleso S obíhá kolem systému těles P a T.

Důsledek 14. Když ale síly NM a ML, když je těleso S velmi daleko, jsou velmi blízké síle SK a poměr spojený poměr PT a ST, tj. jsou-li dány vzdálenost PT a absolutní síla S, jako převrácená hodnota ST³, a tyto síly NM a ML jsou příčinou veškerých poruch a vlivů. o kterých bylo pojednáváno v předchozích důsledcích; proto je zřejmé,že tyto vlivy, pokud systém těles T a P zůstává stejný a mění se jenom vzdálenost ST a absolutní síla tělesa S, jsou velmi blízké poměru vypočteném jako poměr absolutní síly tělesa S a převrácené hodnoty třetí mocniny vzdálenosti ST. V souhlase s tím, když systém těles T a P obíhá kolem vzdáleného tělesa S , tyto síly NM a ML a jejich důsledky budou (podle důsledků 2  a 6 tvrzení 4) nepřímo úměrné čtvercům oběžných dob. A proto také, když velikost tělesa S je úměrná této absolutní síle, tyto síly NM a ML a jejich vlivy  budou v přímém poměru třetí mocniny zdánlivého poloměru vzdáleného tělesa S při pohledu z tělesa T a naopak. Neboť tyto poměry jsou stejné jako výše zmíněný vypočtený poměr.

Důsledek 15. Když jsou velikosti oběžných drah ESE a PAB změněny, zatímco jejich tvar, jejich úměry a vzájemný sklon zůstanou stejné, a když síly působené tělesy S a T též zůstanou stejné nebo se změní v daném poměru, potom tyto síly, tj. síly tělesa T, jehož působením je těleso P vychylováno z přímočaré dráhy na dráhu PAB, a síly tělesa S, jejichž působením je těleso P vychylováno a odchylováno ze své oběžné dráhy„ budou stále působit stejným způsobem a v témž poměru; takový případ bude nutně takový, že všechny vlivy podobné a úměrné a že časy odpovídající tomuto působení budou rovněž úměrné, tj. všechny lineární poruchy budou úměrné poloměrům drah a úhlové poruchy budou stejné jako dříve úměrné oběžným dobám drah těles.

Důsledek 16. A dále, když jsou dány tvary oběžných drah, ale velikosti, síly a vzdálenosti těles jsou jakkoliv změněny, potom z daných poruch a daných časů poruch v jednom případě je možno najít poruchy a časy poruch v libovolném jiném případě velmi snadno. Může to ale být uděláno velmi stručně následující metodou. Síly NM a ML, pokud vše ostatní zůstane stejné, jsou úměrné vzdálenosti TP a jejich časové působení jsou (podle důsledku 2 tvrzení 10) jsou úměrné součinu sil a čtverci oběžné doby tělesa P. To jsou lineární poruchy pohybu tělesa P, a jelikož úhlové poruchy jsou pozorovány z tělesa T (tj. apoapsidy a uzly, stejně jako zdánlivé poruchy v v podélném i příčném směru) a pro každý oběh tělesa P jsou velmi blízké čtvercům oběžných dob. Složením těchto poměrů s poměry z důsledku 14 zjistíme, že v libovolném systému těles T, P a S, ze kterých P obíhá okolo T a je u něj blízko a T obíhá kolem vzdáleného tělesa S [tj. situace, která odpovídá pojmenování bodů na obrázku a ne grafickému znázornění], úhlové poruchy tělesa P pozorovaného z tělesa T budou při každém oběhu tělesa P přímo úměrné čtverci oběžné doby tělesa P a nepřímo úměrné čtverci oběžné doby tělesa T. A tak střední pohyb apoapsidy bude v pevném poměru střednímu pohybu uzlů, a každý z těchto dvou pohybů bude přímo úměrný oběžné době tělesa P a nepřímo úměrné oběžné době tělesa T. Zvětšování a zmenšování výstřednosti a úhlové odchylky orbitu PAB není pohyb apoapsid a uzlů citelně ovlivněno, pokud výstřednost a úhlová odchylka není příliš veliká.

Důsledek 17. Jelikož ale úsečka LM je někdy větší a někdy menší než vzdálenost PT, nechť střední síla LM je představována vzdáleností PT; potom tato síla bude ke střední síle SK nebo SN (která může být představována úsečkou ST) jako délka PT k délce ST. Ale střední síla SN nebo ST, která udržuje těleso T na jeho dráze kolem S, je k síle, kterou je těleso P udržováno na své dráze kolem T, v poměru vypočteném z poměru vzdálenosti ST ke vzdálenosti PT  a čtverce poměru oběžné doby tělesa P kolem T k oběžné době tělesa T kolem S. A z rovnosti poměrů je střední síla LM k síle, která udržuje těleso P na dráze kolem T (nebo působením které by stejné těleso P obíhalo za stejnou dobu kolem nehybného bodu T ve vzdálenosti PT) ve stejném poměru čtverců oběžných dob. Proto, jsou-li dány oběžné doby, spolu se vzdáleností PT, je dána i střední síla LM, a když je, síla MN je s velkou blízká úměrnosti úseček PT a MN.

Důsledek 18. Představme si tekutá tělesa, která se pohybují kolem tělesa T ve stejných vzdálenostech od něj podle stejných zákonů, podle kterých těleso P obíhá okolo stejného tělesa T a nechť prstenec - tekutý, kulatý a soustředný kolem tělesa T, který je vytvořen těmito jednotlivými tekutými částicemi ve vzájemném kontaktu; tyto jednotlivé části prstence, které vykonávají svůj pohyb podle zákonů platných pro těleso P, se přiblíží blíže k tělesu T a budou se pohybovat rychleji v vlastní konjunkci a opozici vůči tělesu S než v kvadraturách. Uzly tohoto prstence neboli jeho průsečík s rovinou dráhy tělesa S nebo T, budou v klidu v syzygách, ale mimo syzig se budou pohybovat dozadu, a to rychleji v kvadraturách a pomaleji v jiných místech. Odchylka prstence se též bude měnit, a jeho osa bude se bude kývat při každém oběhu, a po dokončení oběhu, vrátí se do původní polohy až na to, že je tažen okolo při precesi uzlů.

Důsledek 19. Nyní si představme, že planeta T složená z netekuté hmoty bude tak zvětšená až přesáhne tento prstenec a má příkop naplněný vodou okolo svého obvodu; a představme si, že tato planeta se rovnoměrně otáčí okolo své osy stejnou oběžnou rychlostí. Tato voda, která bude střídavě zrychlována a zpomalována (jako v předchozím důsledku) bude rychlejší v syzygách a pomalejší v kvadraturách než samotný povrch planety, a tak bude odtékat a přitékat příkopem právě tak, jako to činí moře. Pokud odstraníme přitažlivost tělesa S, potom voda obíhající kolem nehybného středu nebude odtékat ani přitékat. Je to jako u planety, která se pohybuje rovnoměrně přímočaře a současně se točí okolo své osy (podle důsledku 5 zákonů). Když těleso S přiblížíme, jeho nerovnoměrné přitahování vody způsobí její rozdělení, neboť bližší vodu bude přitahovat silněji a tu vzdálenější méně. Kromě toho síla LM bude přitahovat vodu dolů v kvadraturách a bude klesat v syzygách a síla KL bude přitahovat tu samou vodu nahoru v syzygách a bude bránit dalšímu stoupání a bude působit její pokles v kvadraturách do té míry, dokud pohyb odlivu a přílivu není ovlivněn vodním příkopem a je poněkud zpožděný třením.

Důsledek 20. Když se prstenec změní na pevný a planeta se zmenší, pohyb odlivu a přílivu ustane, ale kývavý pohyb odchylek a precese uzlů zůstane. Nechť planeta má stejnou osu jako prstenec a uskuteční svou otáčku za stejnou dobu a nechť se její povrch zevnitř dotýká prstence a přilne k němu, potom s přispěním pohybu prstence se bude celý systém kývat a uzly se budou zpožďovat. Neboť planeta, jak již bylo ukázáno, je stejně citlivá ke všem vlivům. Největší úhlová odchylka samotného prstence, pokud vyjmeme planetu, nastane když uzly jsou v syzygách. Odtud při dopředném pohybu uzlů do kvadratur se bude snažit snížit svou úhlovou odchylku a tato snaha zapůsobí na pohyb celé planety. Planeta si zachová tento vynucený pohyb, dokud prstenec nezastaví tento pohyb opačnou snahou a nevynutí si pohyb v opačném směru; a tímto způsobem největší pohyb zmenšující se odchylky nastane, když jsou uzly v kvadraturách, a nejmenší úhlová odchylka nastane v oktantech po kvadraturách; a největší pohyb rostoucí odchylky nastane v syzygách; a největší úhel v příštím oktantu. A podobně je tomu i s planetou, která nemá žádný prstenec a která je v oblasti rovníku buď o něco vyšší nebo z hmoty s větší hustotou. Neboť právě taková převaha hmoty na rovníku nastává u prstence. A i když při rostoucí centrální síle této planety jakýmkoliv způsobem jsou všechny její části taženy dolů jako to činí přitahující části Země, nicméně jevy popsané v tomto důsledku a důsledku 19 budou ztěží měnit toto vysvětlení, až na to, že místa menší a větší výšky vody budou jiná. Neboť voda nyní setrvává a zůstává na své dráze svou vlastní odstředivou silou, ale příkopem ve kterém proudí. A kromě toho síla LM přitahuje vodu dolů nejvíce v kvadraturách a síla KL nebo NM - LM přitahuje tutéž vodu nahoru nejvíce v syzygách. A tyto síly dohromady přestanou přitahovat vodu nahoru a začnou jí jí přitahovat dolů v oktantech po syzygách, Jako důsledek je největší výška vody může nastat zhruba  v oktantech po syzygách, a nejmenší výška vody zhruba v oktantech po kvadraturách, samozřejmě s výjimkou toho,že pohyb této vody při vzestupu nebo poklesu vynuceného těmito silami se buď zachová o něco déle působením setrvačnosti vody nebo se zastaví o něco dříve působením překážek v příkopu.

Důsledek 21. Stejným způsobem jakým přebytek hmoty planety blízko rovníku způsobuje zpožďování uzlů (a toto zpožďování roste s přibýváním hmoty na rovníku a je zmenšováno jeho zmenšováním a je odstraněn při jejím odstraněním) a z toho vyplývá, že když odstraníme více než nadbytečnou hmotu, tj. když je planeta blízko rovníku je buď stlačenější nebo řidší než na pólech, nastane pohyb uzlů dopředu.

Důsledek 22. A naopak z pohybu uzlů je možno zjistit složení planety. Když řekněme planeta stále zachovává stejné póly a nastává zpětný pohyb, má přebytek hmoty na rovníku; když nastává pohyb vpřed, je jí nedostatek.Předpokládejme, že homogenní a přesně kulová planeta je za prvé v klidu ve volném prostoru; potom je postrčena libovolným impulsem přiloženým šikmo k jejímu povrchu, jehož působením se dá do pohybu, který je zčásti rotační a zčásti přímočarý vpřed. Protože tato planeta je neutrální ke každé ose procházející jejím středem a nemá větší tendenci otáčet se okolo kterékoliv osy nebo kolem osy s jakýmkoliv konkrétním náklonem, je jasné, že tato planeta svým vlastním přičiněním nikdy nezmění svou osu a její náklon. Nyní nechť je planeta postrčena šikmo jakýmkoliv jiným novým impulsem, přiloženým k té samé části povrchu jako předtím; potom, jelikož účinek impulsu se v žádném případě nemění ať je přiložen dříve nebo později, je zřejmé, že by působením těchto dvou impulsů vznikl stejný pohyb , kdyby působily současně, tj. výsledný pohyb bude stejný jako kdyby na planetu působila jediná síla složená z těchto dvou (důsledek 2zákonů) a tak se bude pohybovat jednoduchým pohybem okolo osy s určitým náklonem. Podobně jako v případě, kdy druhý impuls působí na jakémkoliv jiném místě rovníku prvého pohybu, a též když prvý impuls působí v kterémkoliv místě rovníku pohybu, který by vyvolal ten druhý impuls bez toho prvého, a tedy pro oba impulsy přiložené kamkoliv. Tyto dva impulsy způsobí stejný rotační pohyb jako kdyby působily dohromady a najednou v průsečíku rovníků obou pohybů, které by každý z nich způsobil samostatně. A tedy homogenní a dokonalá planeta si nezachová několik dílčích pohybů, ale složí všechny působící síly a omezí je na jednu; a dokud může sama o sobě, vždy rotuje jednoduchým a rovnoměrným pohybem okolo jediné osy s daným a vždy neměnným náklonem. A centrální síla nemůže změnit ani tento náklon ani tuto osu nebo rychlost rotace.

Pokud si planetu v duchu rozdělíme na dvě polokoule rovinou procházející středem planety a středem ke kterému síla směřuje, tato síla bude vždy působit na obě polokoule stejně a proto nezpůsobí, aby se planeta, nehledě na její rotační pohyb, odchýlila jakýmkoliv směrem. Když je potom nějaká nová hmota, nahromaděná ve formě hor, přidána k planetě kamkoliv mezi pól a rovník, potom tato hmota svou neustálou snahou vzdálit se od středu pohybu poruší pohyb planety a způsobí, že póly putují po její ploše a neustále opisují kruhy kolem sebe a protějších bodů. A pokud toto ohromné putování pólů nebude korigováno buď umístěním hor na některý z pólů, což způsobí (podle důsledku 21), že uzly rovníku se budou předbíhat, nebo na rovník, což způsobí (podle důsledku 20), že uzlu se budou zpožďovat, nebo nakonec umístěním nějaké další hmoty na druhou stranu osy, které vyváží při pohybu hory, a v tom případě se uzlu budou buď předbíhat nebo zpožďovat podle toho, zda jsou hory blíže k pólům nebo k rovníku.

Tvrzení 67.  Věta 27.

Když předpokládáme stejné zákony přitažlivosti, tvrdím, že vzhledem ke společnému těžišti  O vnitřních těles  P a  T bude vnější těleso  S průvodiči spuštěnými do tohoto středu opisovat plochy přesněji úměrné časům a s drahou bližší tvaru elipsy, která má své ohnisko v tom samém středu, než opisuje okolo nejvnitřnějšího a největšího tělesa T průvodiči spuštěnými k tomuto tělesu. . 

Neboť přitažlivá síla tělesa S od těles T a  P  se skládá do jeho absolutní přitažlivé síly, která míří spíše ke společnému těžišti O  těles T a P  než k největšímu tělesu T, a která je přesněji nepřímo úměrná čtverci vzdálenosti SO než čtverci vzdálenosti ST, jak může snadno nahlédnout každý, kdo o věci pečlivě uvažuje.

Tvrzení 68.  Věta 28.

Když předpokládáme stejné zákony přitažlivosti, tvrdím, že s ohledem na společné těžiště O  vnitřních těles P a  T bude vnější těleso S průvodiči spuštěnými do tohoto těžiště opisovat plochy  téměř úměrné času a dráhy více podobné tvaru elips, které mají své ohnisko v témž těžišti, pokud na nejvnitřnější a největší těleso působí přitažlivá síla stejně jako na ta ostatní, než v případech, kdy není vůbec přitahováno a je v klidu nebo je přitahováno mnohem více nebo mnohem méně nebo se mnohem více nebo mnohem méně pohybuje.  . 

To lze dokázat téměř stejně jako tvrzení 66, ale důkaz je rozvláčnější a proto ho vynechám. Následující úvaha by měla stačit.

Z důkazu posledního tvrzení je zřejmé, že střed ke kterému je těleso S přitahováno oběma silami dohromady je velmi blízko  těžišti obou těles P a T. Kdyby tento střed souhlasil se společným těžištěm těchto dvou těles a společné těžiště  všech tří těles byl v klidu, těleso S na jedné straně a společné těžiště ostatních dvou těles na druhé straně by opisovaly by přesně opisovaly elipsy kolem společného těžiště v klidu. To je zřejmé z druhého důsledku tvrzení 58 ve srovnání s tím, co je dokázáno v tvrzeních 54 a 65. Ale takový přesný pohyb je poněkud porušen vzhledem ke vzdálenosti těžiště obou těles od středu, ke kterému je přitahováno těleso S.  Je-li pohyb navíc dán vzhledem ke společnému těžišti všech tří, a poruch a vzroste. Vzhledem k tomu je porucha nejmenší když je společné těžiště všech tří v klidu, tj. když nejvnitřnější a nejtěžší těleso T je přitahováno podle přesně stejného zákona jako jako ostatní tělesa a stává se větší vždy, když společné těžiště všech tří těles se díky zmenšení pohybu tělesa T začne pohybovat a tedy působí více a více.

Důsledek: A proto, když několik menších těles obíhá okolo tělesa většího, je možno zjistit, že opisované dráhy se budou více přibližovat eliptickým drahám a opsané plochy budou úměrnější času, když se budou všechna tělesa  přitahovat a působit na sebe zrychlujícími silami, které jsou přímo úměrné jejich absolutním silám a nepřímo úměrné čtverci jejich vzdálenosti a pokud je ohnisko každé dráhy umístěn ve společném těžišti všech vnitřních těles (tj. ohnisko prvé a nejvnitřnější dráhy v těžišti největšího a nejvnitřnějšího tělesa, ohnisko druhé dráhy ve společném těžišti dvou nejvnitřnějších těles; ohnisko třetí dráhy ve společném těžišti tří nejvnitřnějších těles atd.), než když je nejvnitřnější těleso v klidu a je pokládán za společné ohnisko všech drah.

Tvrzení 69.  Věta 29.

V systému několika těles A, B, C, D, … libovolné těleso A přitahuje všechna ostatní  B, C, D, … zrychlující silou, která je nepřímo úměrná čtverci vzdálenosti od přitahujícího tělesa; a pokud některé jiné těleso B též přitahuje ostatní tělesa A, C, D, … silami, které jsou nepřímo úměrné kvadrátu vzdáleností od přitahujícího tělesa; potom absolutní síly přitahujících těles A a B budou ve vzájemném poměru jako samotná tato tělesa [tj. jejich hmotnosti]  A a  B, ke kterým tato síla přísluší.  . 

Neboť ve stejných vzdálenostech je urychlující přitažlivost všech těles B, C, D, …. vůči A navzájem rovné podle předpokladu; a podobně, ve stejných vzdálenostech jsou urychlující přitažlivosti všech těles vůči B  jsou si navzájem rovné. Kromě toho, ve stejných vzdálenostech je absolutní přitažlivost tělesa A k absolutní přitažlivé síle tělesa B jako je urychlující přitažlivost všech těles vůči A k urychlující síle všech těles vůči B ve stejných vzdálenostech; a urychlující přitažlivost tělesa B  k A je též  ve stejném poměru jako urychlující přitažlivost tělesa A k B, protože hybná síle, které (podle definic 2, 7 a 8) jsou úměrné součinu urychlující síly a [hmotnosti] přitahovaných těles, jsou v tomto případě (podle třetího pohybového zákona) navzájem rovné. Proto absolutní přitažlivá síla tělesa A je k absolutní přitažlivé síle tělesa B jako hmotnost tělesa A ke hmotnosti tělesa B. Což se mělo dokázat.

Důsledek 1: Proto když každé z jednotlivých těles systému A, B, C, D, … jednotlivě přitahuje ostatní zrychlujícími silami, které jsou nepřímo úměrné čtvercům vzdáleností od přitahovaných těles, absolutní síly těchto těles budou navzájem v poměrech [hmotností] těchto těles samotných.

Důsledek 2: Na základě stejného argumentu, každé z jednotlivých těles systému A, B, C, D, … jednotlivě přitahuje všechna ostatní urychlujícími silami, které jsou přímo nebo nepřímo úměrné libovolné mocnině vzdálenosti přitahovaných těles nebo jsou určeny pomocí vzdáleností mezi přitahovanými tělesy podle zákona společného pro všechna tato tělesa, potom je zřejmé, že absolutní síly těchto těles jsou úměrné [hmotnosti] těchto těles.

Důsledek 3: Jestliže v systému těles, jejichž síly klesají se čtvercem vzdáleností, menší tělesa obíhají kolem větších po elipsách tak přesně, jak je to možné, a mají společné ohnisko v těžišti velkého tělesa a opisují průvodiči spuštěnými k největšímu tělesu plochy úměrné času tak přesně, jak je to možné, potom absolutní síly těchto těles budou navzájem v poměru, přesně nebo tak přesně, jako je to možné, jako [hmotnosti] těles, a naopak. To je jasné z důsledku tvrzení 68 v porovnání s důsledkem 1 tohoto tvrzení.

Komentář

Tato tvrzení nás vedou k analogii mezi centrálními silami a ústředními tělesy, ke kterým síly směřují. Proto je rozumné, aby síly směřující k tělesům závisela na jejich podstatě a na množství hmoty v nich, jako v případě magnetických těles. A kdykoliv nastanou případy tohoto druhu, přitažlivost těles musí být zjištěna přiřazením odpovídajících sil jednotlivým částicím a potom použít součet těchto sil.

Používám zde slovo „přitažlivost“ v obecném smyslu pro jakékoliv jevy, když tělesa na sebe působí, ať už jev nastává jako výsledek působení těles přitahovaných k sobě nebo působících na sebe prostřednictvím emitované energie nebo vzniká působením etheru nebo vzduchu nebo jakéhokoliv jiného media - ať už korpuskulárního nebo ne - jakkoliv, pokud přitahuje k sobě tělesa, která v něm plují. Používám slova „impuls“ v určitém obecném smyslu a pokládám v tomto pojednání ne druhy sil a jejich fyzikální kvalitu, ale jejich velikost a matematickou úměru, jak jsem popsal v definicích.

Matematika vyžaduje zkoumat velikost sil a úměry, které vyplývají z podmínek, které je nutno předpokládat. Proto, když se vrátíme k fyzice, úměry musí být přiřazeny jevům, a je možno zjistit, za jakých podmínek síly působí na každý druh přitahovaných těles. A potom nakonec bude možné bezpečněji pojednávat o fyzikálních druzích, fyzikálních příčinách a fyzikální úměrnosti těchto sil. Podívejme se proto, jaké jsou to síly, kterými kulová tělesa, sestávající s částic, které se přitahují výše zmíněným způsobem, na sebe navzájem působí, a jaký druh pohybu vyplývá s těchto sil.

Sekce 12.

O přitažlivých silách sférických těles .

Tvrzení 70.  Věta 30.

Jestliže ke každému jednotlivému bod kulové plochy přísluší stejné centrální síly klesající se čtvercem vzdálenosti od tohoto bodu, tvrdím, že částice umístěná dovnitř plochy nebude přitahována těmito silami žádným směrem . 

Nechť HIKL je kulová plocha a  P částice umístěná uvnitř. Bodem P veďme k této ploše dvě čáry HK a  IL vytínající malé oblouky HI a KL; a protože trojúhelníky HPI a  LPK jsou si podobné (podle důsledku 3 lemmatu 7), tyto oblouky budou úměrné vzdálenostem HP a LP, a libovolné části sférické plochy v  HI a KL, ukončené kdekoliv úsečkami procházejícími bodem P, budou mít poměr velikostí rovný čtverci tohoto poměru. Proto síly působící na těleso P těmito částmi jsou stejně veliké, protože jsou úměrné velikosti částí a nepřímo úměrné čtverci vzdáleností, a složením těchto poměrů dostaneme rovnost. Proto přitažlivosti mající stejnou velikost a opačný směr se vzájemně vyruší. Na základě stejných argumentů se vzájemně zruší přitažlivost všech částí kulové plochy přitažlivostí protějšku. Proto není těleso P přitahováno nikam. Což se mělo dokázat.

Tvrzení 71.  Věta 31.

Za stejných podmínek jako u tvrzení 70, tvrdím, že částice umístěná mimo kulové plochy je přitahována ke středu koule silou nepřímo úměrnou čtverci vzdálenosti od tohoto středu. . 

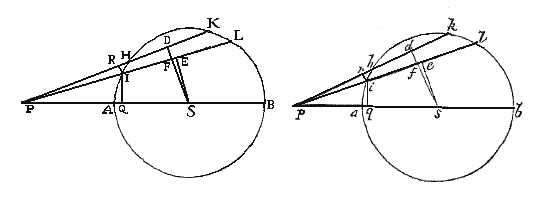Nechť AHKB a ahkb jsou stejné sférické plochy opsané kolem středů S a s o průměrech AB a ab, nechť P a p jsou částice umístěné vně těchto koulí na prodlouženích těchto průměrů [tj. vzdálenosti PS a ps se liší, výpočet závislosti na vzdálenosti od středu]. Z částic vyneseme přímky PHK, PIL, phk a pil tak, aby odřízly z velkých kružnic AHB a ahb stejné oblouky HK a hk a IL a il. A k těmto přímkám sestrojme kolmice SD a sd, SE a se, IR a ir, z nichž SD a sd  protnou PL a pl v bodech F a f. Spusťme též kolmice IQ a iq  na tyto průměry. Nechť se úhly DPE a  dpe mezně zmenšují [např. tak, že HK a hk jsou pevné, IL a il se k nim přibližují]; potom, protože DS a ds, ES a  es budou stejné, úsečky PE, PF a  pe, pf a úsečky DF a  df je možno pokládat za stejné, přinejmenším v jejich mezním poměru, když úhly DPE a  dpe současně vymizí, jsou si rovny.

Na základě toho bude proto PI  k  PF jako RI  k  DF  a dále pf  k pi  jako df  nebo DF  k ri; vynásobením dostaneme, že PI × pf  bude k PF × pi  jako RI  k ri, tj. (podle důsledku 3 lemmatu 7) jako oblouk IH  k oblouku ih. Dále PI  bude k  PS  jako IQ  k  SE  [podobnost △ PIQ a PSE ] a  ps bude k  pi jako se nebo SE  k  iq  [podobnost △ pes a pqi ]; a vynásobením poměrů dostaneme, že PI × ps  bude PS × pi  jako IQ  k iq. A složením těchto poměrů PI² × pf × ps bude k pi² × PF × PS  jako IH × IQ  k ih × iq; tj. jako kulová plocha kterou oblouk IH opíše při otáčení polokružnice AKB  kolem průměru AB  ke kulové ploše, kterou oblouk ih opíše při rotaci polokruhu akb kolem průměru ab. A síly kterými tyto plochy přitahují částice P a p (podél přímek směřujícím k těmto plochám) jsou (podle předpokladu) přímo úměrné těmto plochám a nepřímo úměrné vzdálenosti těchto ploch od těles, tj. jako pf × ps k  PF × PS.

A tedy (když rozklad sil je proveden v souhlase s důsledkem 2 zákonů), tyto síly jsou k jejich šikmým složkám, které směřují podél přímek PS a ps do středu, jako PI  k  PQ a  pi k pq; tj. (protože trojúhelníky PIQ a  PSF jsou podobné), síly jsou ke svým šikmým složkám jako PS  k  PF a  ps k pf. Proto z rovnosti poměru přitažlivost částice P  k  S  bude k přitažlivosti částice p k  s v poměru k , tj. jako ps²  k PS². A na základě podobných argumentů jsou síly, kterými plocha opsaná rotací oblouků KL a kl přitahovat částice v poměru ps²  k PS². A stejný poměr bude platit pro síly každé ze dvou kulových ploch, na které je možno obě koule rozdělit, když pokaždé položíme sd rovné SD a se rovné SE. A složené síly, kterými celá kulová plocha působí na částice, budou ve stejném poměru. Což se mělo dokázat.

Poznámky

Přechod na domovskou stránku